Contexte et notations
Dans le chapitre 2 sur les énergies (exemple 3), la conservation de l'énergie mécanique totale seule ne permet pas de résoudre le mouvement dans l'espace à
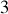dimensions d'une seule particule (problème à 1 corps) soumise à une force centrale... sans pousser plus loin l'investigation.
Ce problème est repris ici sous une forme initialement plus complexe puisqu'il s'agit de
corps en mouvement et en interaction.
En effet, cette étude peut être ramenée dans le cas d'un champ central à un problème à un corps dans le cas général et pas seulement moyennant une approximation portant sur le rapport des masses.
De plus le mouvement à un corps, et donc à deux corps, est ici résolu.
Dans ce chapitre, le système est constitué de deux particules (de masses
ou charges
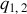), cette étude étant valable autant pour la gravitation que pour l'interaction électrique. Il est fermé.
Ces particules interagissent entre elles au moyen de forces réciproques, centrales et portées par l'axe reliant les 2 particules, orienté de 1 vers 2. (fig.18)
L'amplitude des forces est notée
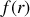(> ou <0, cas d'attraction ou répulsion).
Elle dérive de l'énergie potentielle suivante :
.
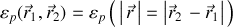Elle est issue de forces réciproques (
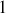s'appliquant sur
et
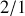) du type :
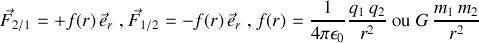
telles que représentées sur la fig. 18 dans le cas d'une attraction.
Méthode : Système fermé et CDM
Les équations du principe fondamental appliqué à chaque particule s'écrivent :
Pour dériver les positions de chaque particule dans l'espace, (→
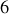coordonnées inconnues),
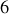équations du second ordre couplées par
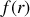restent à intégrer, nécessitant
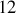conditions initiales.
Mais la forme centrale de l'interaction met en évidence des propriétés qui vont être exploitées pour simplifier le problème.
Ces propriétés découlent toutes de l'observation directe suivante : la somme des deux équations du mouvement ci-dessus met en évidence la dérivée temporelle nulle de la quantité de mouvement totale.
Cette grandeur se trouve être également la dérivée du centre de masse (CDM) du système des deux corps.
Ainsi le CDM joue un rôle particulier... puisque sa quantité de mouvement est vectoriellement constante.
Comme pour les chocs.
Deux points essentiels émergent :
le CDM a un mouvement rectiligne uniforme et
la caractéristique réciproque et centrale de l'interaction dans sa dimension vectorielle mais également dans sa dépendance spatiale en module de la distance relative.
Ils vont orienter l'étude vers le CDM comme pour le cas du choc et vers une variable de mouvement relatif porté par le type d'interaction.
