i. Le changement de variables
Du fait de la forme de l'interaction, le couple de vecteurs (
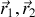) peut être remplacé par un nouveau couple de variables (
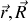) défini par :
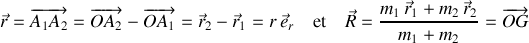
La position relative
est associée au vecteur
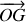décrivant le mouvement du centre de masse.
Si ce nouveau couple de vecteurs est connu, le retour aux coordonnées réelles est aisément obtenu à l'aide de :
Ces dernières formules mettent en évidence le mouvement relatif de chaque masse
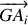dans le référentiel du CDM lesquels ne dépendent que d'une seule variable... la position relative
.
Dans ce référentiel, elles vont l'une vers l'autre, de front, mais avec des vitesses pondérées par les masses.
Fondamental : Le mouvement relatif
L'intérêt mathématique de ce changement de variables est de réduire le nombre d'inconnues du problème.
Le mouvement de
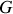est complétement déterminé puisque, suite à l'application du PFD au système des deux corps (
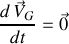), il est rectiligne et uniforme. Seul reste donc à étudier le mouvement décrit par la variable
. Le point
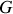devient également un bon candidat pour devenir le sommet d'un référentiel galiléen.De surcroît la position relative peut être rapportée à
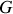au moyen de :
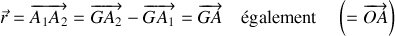
Résoudre le mouvement décrit par
revient à déterminer le mouvement du point
, un point matériel fictif dont le rayon vecteur est justement
.L'équation du mouvement relatif suit :
Cette équation représente le PFD appliqué à la particule fictive
repérée par rapport à
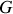, de masse
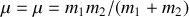, la masse réduite, et soumise à la même force centrale que la particule
.
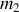Remarque :
A ce niveau, le problème à 2 corps soumis à une interaction réciproque centrale a été réduit à un problème à 1 corps unique, représenté par la particule fictive repérée dans un référentiel galiléen de centre le CDM des 2 corps.
Cette particule est soumise à la force centrale initiale.
Le centre
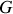et le point fictif
sont sur la ligne
.
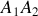Le vecteur
est porté par la ligne
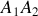dans l'espace de sommet
.
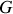Remarque :
Cette description dans le référentiel du CDM est à mettre en parallèle avec celle développée pour le choc 2D.
Elle permet d'extraire le mouvement du centre de masse.
Le retour aux coordonnées initiales des deux particules
le réintroduit selon les formules de retour ci dessus.
Complément : Rapports de masses particuliers
Un cas particulier remarquable concerne la situation où un des deux corps est beaucoup plus massif que l'autre : par exemple
.
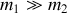Dans ce cas particulier, le CDM est quasi confondu avec la cible : ici le corps le plus lourd. Il en prend la vitesse et la particule fictive correspond alors à la plus légère des 2 masses.
Ce cas particulier décrit l'interaction gravitationnelle telle qu'elle est appréhendée pédagogiquement en première année de Licence pour décrire l'attraction gravitationnelle (sondes, comètes, fusées...).
Cette inégalité de masse est utilisée pour envoyer les sondes de plus en plus loin dans l'espace par collision avec des planètes massives.
La conservation de la quantité de mouvement totale, avant et après la collision, répartit les variations de vitesse en fonction des masses et en signes opposés.
Si le corps massif est en mouvement, la particule légère rebondit sur la cible avec une vitesse supérieure en module à celle de son incidence.
Un autre cas d'école est constitué par deux masses égales.
Le CDM est alors équidistant des deux corps. Les relations ci dessus se trouvent simplifiées.
Pour résoudre le problème de la particule fictive ou problème réduit (de 6 à 3 dimensions), le théorème du moment cinétique reste à exploiter.
Puis deux formes de résolution seront présentées : l'une est une intégration directe des équations, la seconde est plus visuelle et graphique.
ii. Le moment cinétique
Le transfert du problème vers le mouvement relatif pose la question de l'expression du moment cinétique dans le nouvel espace fictif.
Le moment cinétique total par rapport à
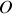est une grandeur conservée.
Son expression en fonction de
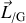a permis de déduire la conservation du moment cinétique total par rapport à
.
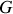Ce dernier, défini par :
,
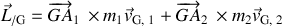n'est rien d'autre que le moment cinétique de la particule fictive.
En effet, la définition barycentrique du CDM permet de déduire que
.
Ainsi :
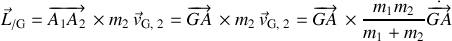
est le moment cinétique de la particule fictive.
Comme signalé précédemment (relation entre les moments cinétiques
et
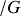) il est conservé.
Cette propriété vectorielle est à l'origine des 3 caractéristiques suivantes (lois de Kepler) du mouvement dans un champ de force central :
la trajectoire de la particule fictive est plane, puisque le moment cinétique est à chaque instant perpendiculaire à la trajectoire donnée par le couple (
). Si la direction du moment cinétique est fixe, le plan de la trajectoire l'est également. C'est le plan de l'écliptique des planètes et autres mouvement électroniques.
La trajectoire est toujours parcourue dans le même sens.
Le module du moment cinétique est constant, entraînant une relation une relation supplémentaire entre les deux coordonnées décrivant le mouvement plan.
S'agissant d'un moment cinétique, les coordonnées polaires sont les plus adaptées pour la description et le module s'écrit :
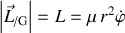.Il est constant.
Cette égalité est aussi connue sous la forme de ‘vitesse aérolaire' ou vitesse surfacique
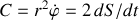.La variation au cours du temps de la surface balayée par le rayon-vecteur.
Celle-ci est constante et exprime une augmentation de la vitesse du mouvement quand la trajectoire se rapproche du centre du champ : objet de la 2nde loi de Kepler.
La conservation du vecteur ‘moment cinétique' dans un champ de force central permet ainsi de réduire le problème de 3 dimensions (variables ou degrés de liberté) à une seule,
: en direction→ mouvement plan (3-1=2), en module→ (2-1).
Pour résoudre la dimension qui reste, il faut préciser le type de l'interaction.
Le développement qui suit concernera le cas, plus riche, de l'attraction gravitationnelle.
Ce cas décrit également l'attraction coulombienne entre deux charges de signes opposées (liaisons atomiques et moléculaires) au détriment de la répulsion des charges identiques (diffusion de type Rutherford) qui peut faire l'objet d'un exercice.
