Des solutions coniques
La force de liaison centrale selon
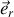s'écrit :
.
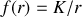L'équation du mouvement issue du PFD appliqué à la particule fictive :
.
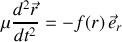En coordonnées polaires et avec
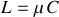, l'équation du mouvement est :
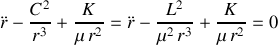
Elle peut être résolue par un changement de variable ‘de Binet' :
.
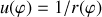En utilisant les 2 relations suivantes :
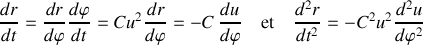
l'équation du mouvement prend la forme :
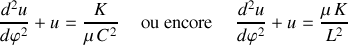
La solution générale est de type :
où
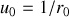et
sont associés aux positions initiales (CI).
Cette solution est identique à :
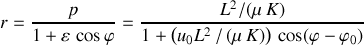
qui représente la forme polaire des coniques.
L'excentricité
dépend des CI souvent données en fonction de l'énergie initiale (voir ci-après) et le paramètre de la conique,
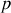, est complétement déterminé.
Ainsi pour le cas de l'attraction gravitationnelle, les expressions respectives des paramètre et excentricité sont :
Et pour assurer une racine réelle dans l'expression de l'excentricité
, l'énergie mécanique initiale
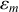peut prendre des valeurs négatives (trajectoires elliptiques, états liés) avec une valeur de seuil (minimum).
Remarque :
Étant donné que
représente le mouvement de la particule fictive de masse
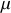dans le référentiel du centre de masse des 2 corps initiaux, le problème est complétement résolu pour chaque corps.
Il suffit d'intégrer la translation rectiligne uniforme du CDM ainsi que les coefficients multiplicatifs (pondération des masses) du changement de variables initial.
Les conditions ci dessus sur les valeurs de l'énergie mécanique initiale suggère l'utilisation de cette grandeur physique : une constante du mouvement.
Elle donne lieu à la représentation graphique qui suit.
