Les résolutions graphiques présentent l'intérêt de visualiser, de donner des images des solutions.
Cette méthode graphique s'appuie sur une propriété de conservation du problème à deux corps.
Conservation de l'énergie mécanique de la particule fictive
Le système des deux masses est fermé : l'énergie mécanique totale est conservée.
Dans le nouveau système de coordonnées, l'énergie cinétique totale s'écrit :
Elle présente deux termes, l'un relatif au mouvement du CDM et qui est constant, le second est l'énergie cinétique de la particule fictive seule.
La conservation de l'énergie mécanique totale, à une constante près, ne concerne donc plus que la particule fictive.
Elle s'écrit :
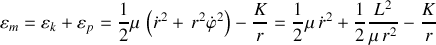
où :
la conservation du moment cinétique a été utilisée.
et l'énergie potentielle du système d'interaction entre les deux corps est identique à celle de la particule unique.
Une énergie potentielle effective apparaît :
Cette énergie mécanique est conservée et dépend de sa valeur initiale.
L'énergie mécanique totale de la particule fictive est également constituée d'une balance de 2 termes :
une énergie cinétique ‘radiale' de la particule fictive, toujours positive, et
une énergie potentielle effective constituée également de 2 termes,
celui issu de la rotation (et du moment cinétique) et
la contribution de l'interaction.
Le mouvement de la particule ne peut avoir lieu que si son énergie cinétique radiale est positive.
L'inégalité suivante
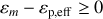, principalement paramétrée par l'énergie initiale, doit être vérifiée.
L'exploitation de cette inégalité pour différentes conditions initiales de l'énergie constitue l'étude graphique proposée.
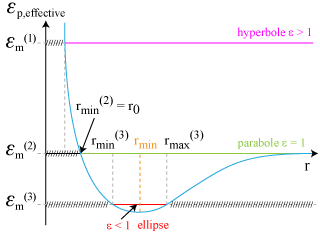
Sur la figure ci-après (fig. 19), l'énergie potentielle effective est représentée en fonction de
.
Elle présente deux comportements asymptotiques remarquables :
Lorsque
tend vers zéro, la contribution en
est dominante, par valeurs positives, alors que
pour
tendant vers
, c'est celle en
qui l'emporte ET par valeurs négatives.
Entre ces deux limites, l'énergie effective s'annule en
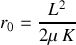et un minimum a lieu pour :
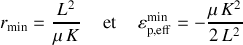
Trois situations d'énergie initiale suffisent à décrire tous les cas de figure.
Sur la fig. 19, ces trois cas ont été représentés, notés respectivement
(1) pour une énergie mécanique positive.
Pour vérifier l'inégalité des énergies, la particule fictive décrit une trajectoire ouverte, hyperbolique, entre une valeur de minimale de
et
.
(2) nulle.
La trajectoire est également ouverte et parabolique : elle représente un cas limite entre les situations (1) et (3).
(3) négative.
La particule est "satellisée".
Elle décrit une ellipse, fermée entre deux valeurs de
. Si l'énergie initiale s'approche du niveau minimal de l'énergie potentielle effective, le mouvement de la particule sera plus harmonique et la trajectoire plus circulaire.
Ces trois cas de figure représentent l'ensemble des situations que peut décrire par exemple une comète au voisinage d'une planète.
L'énergie initiale est représentée par la vitesse linéaire initiale et le paramètre d'impact, la distance d'écart entre les deux trajectoires initiales, supposées parallèles.
Dans ce cas, la zone d'impact est celle où la comète s'approche de la cible avant
soit de la quitter
soit d'y être satellisée.
Si l'énergie de la comète est inférieure à l'énergie minimale, la chute sur la planète est inéluctable.
Dans le cas d'une répulsion électrique, comme la diffusion de Rutherford, la particule incidente s'écarte systématiquement de la cible à l'entrée de la zone d'impact.
Les trajectoires sont toujours ouvertes (libres) avec une distance minimum d'approche.
Dans les zones hors interaction (hors collision) le mouvement est toujours rectiligne et uniforme pour les 2 corps, allant (s'éloignant) l'un vers (de) l'autre.
Le problème à deux corps, dans les deux situations de chocs ou de collisions, ayant été abordé, l'étape suivante dans le cheminement vers le problème à
corps est la théorie de la diffusion.
