Le vecteur moment cinétique d'un solide
Le moment cinétique, par définition, décrit uniquement les rotations. Celles-ci ont lieu par rapport à des axes du solide.
De même il est évalué par rapport à un point du solide.
L'expression du moment cinétique rapportée à un centre donné est la même quel que soit le centre.
L'écriture adoptée dans ce qui suit est donc valide quel que soit le point du solide utilisé : les ajustements et transferts, s'ils s'avèrent nécessaires, seront réalisés au fur et à mesure.
Notations adoptées :
Le choix du CDM parait le plus simple pour des raisons pratiques, y compris relatives aux mouvement du solide et qui seront explicitées plus loin.
De surcroît et suite aux rappels précédents, le transfert vers tout autre point du solide est possible et direct.
Le solide est considéré comme un système de points discrets notés
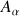; le passage au continuum sera effectué sur les exemples.
Le moment cinétique total dans un référentiel mobile, associé au CDM, s'écrit :
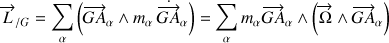
où les rotations sont prises en compte dans l'expression des vitesses.
Si le double produit vectoriel est développé selon la formule :
,
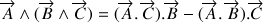l'expression finale du moment cinétique peut être posée selon la forme simplifiée suivante :
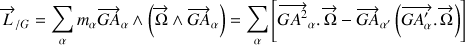
Pour dériver le cas le plus général en termes des
rotations effectuées dans l'espace, une base orthonormée quelconque associée au solide est adoptée :
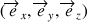centrée ici sur
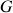, ou sur tout autre point du solide utilisé.
Le vecteur rotation est alors projetée :
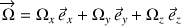
et la position de chaque point exprimée selon
.
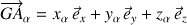L'évaluation de chacun des termes du moment cinétique devient alors systématique. permet de mettre en évidence une forme tensorielle notée
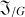, calculée ici par rapport au CDM.
L'expression du moment cinétique en fonction de la vitesse angulaire est linéaire :
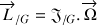
La forme tensorielle s'écrit selon la forme générale suivante et cela quel que soit le centre :
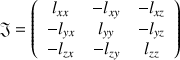
Les termes diagonaux sont les moments d'inertie par rapport aux axes, notés en indice : une formulation reconnaissable par le carré de la distance de chaque point à l'axe.
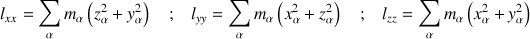
Les termes non diagonaux sont tels que :
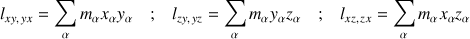
Non nuls, la présence de ces termes indique que les axes (
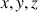) choisis pour le développement ne sont pas des axes de symétrie du solide : les intégrales, issues du passage au continu, vont rapidement pointer ce détail.
Une généralisation de ce tenseur à un système cartésien, d'axes (
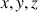) et de centre
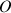quelconque suit.
Fondamental :
Le système d'axes cartésiens, orthonormés, liés au solide étant noté
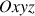, tous les éléments constituant le solide sont repérés par leurs coordonnées.
Le moment cinétique par rapport à un centre
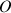du solide, pouvant être le CDM
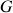, s'écrit donc en toute généralité :
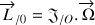
Le vecteur vitesse angulaire, noté
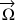, est caractérisé par ses composantes selon les
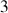directions du référentiel choisi et
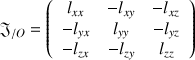
Le tenseur
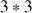d'inertie
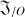est ainsi évalué dans la base cartésienne.
Chaque élément du tenseur représente une somme sur tous les points composant le solide selon deux types :
Les éléments diagonaux du tenseur représentent des moments d'inertie par rapport aux axes
,
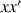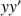et
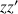. Ils sont définis comme la somme des produits de la masse de chaque point par le carré de leurs distances respectives à l'axe en question : ainsi la distance de
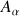à l'axe
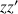est
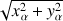.Les termes hors diagonale, constitués de produits de coordonnées de
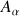, pondéré chacun par la masse du point, possèdent deux propriétés découlant de leur expression :ils sont égaux par permutation des indices : propriété issue de la commutativité du produit.
ils s'annulent lorsque le choix des axes correspond aux symétries du solide : une propriété issue des intégrales de fonctions impaires entre des bornes symétriques.
Les propriétés de symétrie du solide, associées aux simplifications des éléments du tenseur, introduisent de nouvelles notions.
Définition : Axes propres ou principaux d'un solide
Les axes propres, ou axes principaux, d'un solide sont les directions qui diagonalisent le tenseur d'inertie.
Ces axes correspondent aux axes de symétrie du solide et sont caractérisés par leur base unitaire notée
.
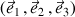Sur le plan pratique :
Ces axes principaux ou axes propres sont des axes de symétrie : ils se croisent au centre de masse (ou de gravité).
Ceci justifie le choix initial de cette origine : l'expression du tenseur en est simplifiée.
De plus, les rotations naturelles d'un solide s'effectuent le plus souvent autour de ses axes propres.
Les directions des axes principaux étant connues, le passage à une autre origine est effectué au moyen du théorème des axes parallèles, ou de Huygens ou de Steiner, qui suit.
