Théorème des axes parallèles
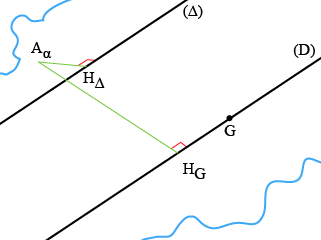
Il existe une relation entre les moments d'inertie par rapport à deux axes parallèles distants de
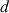et dont l'un passe par le centre de masse : c'est le théorème de Huygens. (Fig. 4)
Théorème :
Dans un solide de masse
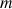, si deux axes sont parallèles et distants de
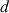, dont l'un,
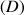, passe par le centre de masse G et le second est noté
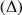, leurs moments d'inertie respectifs sont reliés par la relation :
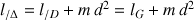
Cette modification correspond à une augmentation du moment d'inertie (par rapport à
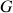) d'une grandeur constante.
Démonstration :
Les deux moments d'inertie sont respectivement définis par :
Suivant la relation vectorielle (de Chasles) :
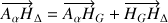, le moment d'inertie recherché est développé selon :
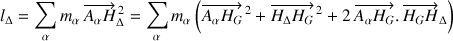
Le dernier terme, sous forme de produit scalaire, s'annule.
En effet,
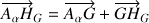
Chacune des contributions s'annule respectivement parce :
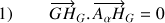
les vecteurs sont orthogonaux, ainsi que :
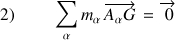
qui est la définition barycentrique du CDM.
Ainsi connaissant le moment d'inertie par rapport à l'un des axes, celui par rapport à l'autre axe peut être déduit.
Complément :
L'utilité d'un tel transfert sera utile lors du calcul du théorème du moment cinétique ou celui de l'énergie cinétique du solide, effectués plus loin.
Par exemple, quand une rotation est identifiée, l'axe de rotation naturel est souvent un axe de symétrie passant par
.
L'existence d'un axe instantané de rotation, parallèle à l'axe de rotation réel, permet alors de simplifier certaines formules et de mettre en évidence l'origine de la rotation (exemples du roulement du cylindre ou de la sphère).
Le parallélisme des axes, dans ce théorème, est mieux compris lorsqu'il est associé à la vitesse angulaire et à son caractère absolu pour le solide : des directions identiques à celle de l'axe de rotation conservent la vitesse angulaire ainsi que le moment associé (cinétique).
De fait, ce transfert entre axes parallèles a un effet uniforme sur le mouvement plan (perpendiculaire à l'axe de rotation) qui en résulte pour chaque point matériel. Ceci explique la différence constante entre les deux moments.
Intuitivement, le passage d'une rotation par rapport à un axe ne passant pas par le CDM produit un effet inertiel supérieur et une vitesse angulaire de rotation potentiellement plus faible.
