L'énergie cinétique de rotation
L'énergie cinétique de rotation est isolée et se présente toujours sous la même forme.
Cette forme caractéristique de "produit vectoriel élevé au carré" est néanmoins tributaire du point
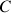utilisé.
Ceci ne perturbe en aucun cas le calcul qui suit.
Une forme compacte de cette énergie peut être obtenue lorsque les sommations sur les masses et la géométrie du solide sont intégrées.
Méthode :
Le terme de rotation est évalué en considérant le carré vectoriel comme un produit scalaire de forme générale :
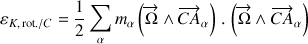
Un produit mixte apparaît où les permutations suivantes seront réalisées :
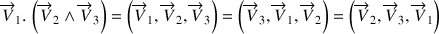
Cette opération permet d'extraire une vitesse angulaire à la sommation pour obtenir :
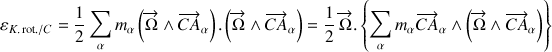
Le terme entre accolades est le moment cinétique rapporté au centre
.
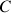La formule du double produit vectoriel peut être appliquée :
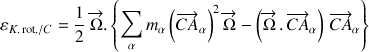
Finalement l'énergie cinétique de rotation évaluée par rapport à un point
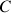s'écrit :
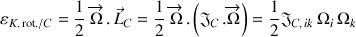
La notation tensorielle a été introduite (sommation sur les indices répétés) et
.
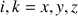Ces grandeurs physiques, moment cinétique et énergie cinétique, ainsi que les notions qu'elles sous-tendent comme les axes propres, les moments d'inertie, le CDM ou centre d'inertie..., sont incontournables pour décrire le mouvement d'un solide dans l'espace.
Étant mis en place, les équations du mouvement du solide peuvent être établies selon les deux formalismes : vectoriel et lagrangien.
Explication :
Dans ce qui vient d'être développé, tous les cas de figures sont présentés, en centre et en axes.
L'intérêt d'utiliser le CDM ou l'axe instantané de rotation apparaissent comme des niveaux différents de simplification, choix d'aubaines mais également démarches pédagogiques.
Le terme de rotation pure est adaptable aux choix effectués puisque les rotations sont des vecteurs, susceptibles d'être projetés, et le tenseur d'inertie présente des modularités.
