Il exprime le théorème précédent mais dans le cas statique.
Règle : ou principe
Dans un déplacement virtuel quelconque, les travaux des forces extérieures compensent ceux des réactions des supports.
Les points de contact sont ici considérés à l'équilibre.
Le déplacement est imaginé sous la contrainte directe du contact.
Exemple :
Dans ces quelques exemples de déplacements réels et de forces de contact, la réalité du déplacement permet de déduire le travail effectué par les forces.
Pour un pendule simple, la contrainte (mouvement circulaire) est générée par la force de liaison : la tension du fil. Elle est toujours perpendiculaire au déplacement.
Sur un vélo, la réaction du sol est perpendiculaire à la surface de contact.
Dans un virage, le cycliste s'incline. Une composante horizontale centripète apparaît pour "compenser" la force d'inertie centrifuge due au virage. Toutes les forces, contact, liaison et inertie, sont perpendiculaires au déplacement
La bille dans un rail qui tourne à la vitesse angulaire
 autour de l’axe vertical ou la fronde (lancer du marteau) sont des exemples de systèmes ouverts (contrainte rhéonome).
autour de l’axe vertical ou la fronde (lancer du marteau) sont des exemples de systèmes ouverts (contrainte rhéonome).Pour la bille, son mouvement a lieu sur la bordure opposée au sens de la rotation ce qui canalise son mouvement dans le rail.
Autrement et en l'absence de cette bordure, la bille resterait en place au démarrage du rail.
- Pour la fronde tenue à bout de bras de lanceur, la sollicitation sur le bras permet de déduire les forces qui s'exercent en fonction du mouvement donné à la fronde.
Et d'ajuster le tir.
Noter que tous les mouvements, imaginés et non, restent alignés sur la contrainte.
Dans les démonstrations qui suivent,
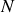 particules sont considérées, repérées par un indice
particules sont considérées, repérées par un indice
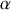 variant de
variant de
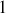 à
à
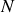 .
.
Quant aux
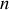 degrés de liberté relatifs aux coordonnées généralisées, ils seront indicés par
degrés de liberté relatifs aux coordonnées généralisées, ils seront indicés par
 , lequel varie de
, lequel varie de
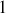 à
à
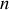 .
.
Un premier travail consistera à établir des relations de passage entre les variables réelles et celles généralisées.
Puis les particules étant soumises à des forces, le principe des travaux virtuels sera appliqué, selon les caractéristiques des forces.




