La transformation de l'accélération généralisée s'effectue en trois étapes, détaillées ci-après.
1) Utiliser la dérivée temporelle de la vitesse
telle que issue de la dérivée d'un produit.
Ainsi l'écriture suivante de l'accélération généralisée :
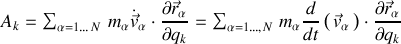
permet l'écriture en deux contributions suivante :
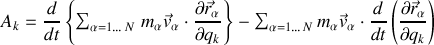
Chacun des deux termes ci-dessus s'exprime en fonction de l'énergie cinétique, moyennant l'utilisation de deux propriétés explicitées ci-après.
Méthode :
La première propriété est déduite en appliquant à la vitesse la forme générale de la dérivée temporelle d'une fonctionnelle.
La durée du déplacement virtuelle étant nulle, le temps n'est pas explicite.
Et l'expression de la position, passée en termes de variables généralisées, permet de déduire la propriété suivante :
obtenue par identification des composantes du développement, terme à terme.
Cette propriété introduit la dérivée temporelle simultanément au numérateur et dénominateur (ou la simplifie).
Pour la seconde propriété : la dérivée temporelle suivante est également développée sous forme de fonctionnelle :
qui permet d'isoler la dérivée partielle en
de la sommation et de reconnaître la vitesse de chaque particule.
Cette dérivée temporelle produit donc une contribution en termes de vitesses sous la forme d'une dérivée partielle :
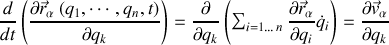
Cette propriété représente une sorte de permutation entre dérivée temporelle et dérivée partielle "généralisée.
Ces deux propriétés font émerger chacune des dérivées partielles de la vitesse particulaire
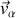pouvant être utilisées chacune dans un terme de l'accélération généralisée.
C'est l'objet de la seconde étape.
2) Le premier terme de l'accélération généralisée permet de mettre en évidence une différentiation de l'énergie cinétique totale autorisant l'écriture suivante
La dérivation partielle de la vitesse dans l'espace de coordonnées généralisées peut être mise en facteur :
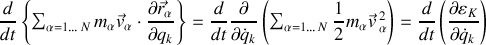
Ce premier terme de l'accélération généralisée trouve ainsi sa source dans l'énergie cinétique.
La dernière étape consiste à utiliser la seconde propriété dans le second terme de l'accélération généralisée.
3) Dans le second terme, est reportée l'expression de la dérivée temporelle permettant l'apparition de dérivée de la vitesse telle que :
ou en termes d'énergie cinétique :
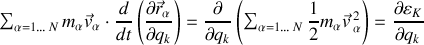
Ainsi l'accélération généralisée peut être complétement exprimée en fonction de l'énergie cinétique du système.
Fondamental :
L'expression de l'accélération généralisée s'exprime en fonction de l'énergie cinétique du système étudié,
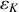, sur laquelle s'applique un opérateur différentiel.
Elle s'écrit :
où, en toute généralité, l'énergie cinétique est :
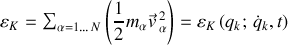
pour un système de
particules de masses
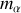évoluant avec des vitesses
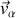dans l'espace réel.
Étant dérivées dans le système de
variables généralisées, cette énergie cinétique est exprimée dans ce système :
.
Le théorème des travaux virtuels permet alors de déduire, dans l'espace des variables généralisées, les relations entre accélérations et forces généralisées :
Ainsi le transfert sur les variables généralisées est complétement réalisé.
Complément : Statique et Principe de d'Alembert généralisé
Avant d'aborder le traitement au cas par cas des types de forces généralisées, la question de la statique du mouvement se pose dès à présent et peut être résolue.
La partie cinétique est contenue dans l'accélération généralisée. Si cette dernière est nulle, une forme de « principe d'inertie » en termes de coordonnées généralisées est obtenue.
Principe de D'Alembert généralisé :
En l'absence de mouvement et en cas d'équilibre, l'énergie cinétique est nulle entraînant la nullité de l'accélération généralisée.
Ceci implique :
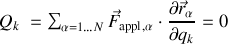
produisant
équations scalaires.
Attention :
Il y a autant d'équations que de degrés de liberté.
Il s'agit là d'une somme sur des grandeurs réelles, donc des projections et non pas de forces vectorielles, au sens habituel.
En mécanique, la position peut être une distance dans une direction donnée ou un angle. Les coordonnées généralisées peuvent avoir ces deux caractéristiques.
Les forces généralisées associées peuvent être soit une force soit un moment de force.
L'objectif du formalisme lagrangien étant de résoudre les mouvements, ces dernières relations sont assez peu utilisées, le formalisme vectoriel des forces étant plus … réel, visuel. Géométrique.
A présent deux remarques relatives
à la particule libre et
aux systèmes de références en mécanique
peuvent apporter un éclairage complémentaire.
Remarque : Cas particulier de la particule libre
Lorsque la résultante des forces appliquées est nulle, les forces généralisées s'annulent. L'équation décrivant le mouvement de la particule libre est :
entraînant de fait une énergie cinétique constante.
Le lagrangien de la particule libre est obtenu par comparaison avec les équation d'Euler Lagrange. Il correspond ici en toute généralité à
.
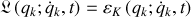Complément : Forme générale de l'énergie cinétique
L'écriture de l'énergie cinétique en coordonnées généralisées
dépend des relations de passage des coordonnées
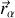de l'espace réel.
Ces relations dépendent des contraintes subies par le système ; elle peuvent également dépendre du temps.
Ceci explique la notation générale
.
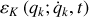De fait, en mécanique et pour les problèmes présentant des solutions (intégrables), le temps n'apparaît pas dans l'énergie cinétique.
Elle s'écrira d'après les relations de passage et de façon générale pour une particule :
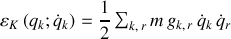
où
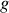est un tenseur
pouvant dépendre des variables
.
Pour les systèmes de coordonnées définissant la métrique dans l'espace réel, l'accélération généralisée n'est rien d'autre que l'accélération réelle pour le système de coordonnées cartésiennes et
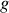est le tenseur unité.
Exemple : Cas des coordonnées sphériques
En coordonnées sphériques par exemple, dans ce référentiel mobile, l'énergie cinétique s'écrit :
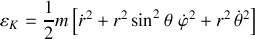
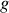est diagonal et dépend du couple
.
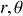L'accélération généralisée contient l'accélération selon la direction ou l'angle considéré mais également les accélérations d'inertie ou d'entraînement obtenues avec l'opérateur
.
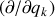Le lagrangien de la particule libre ne dépendant que de l'énergie cinétique, il a été le premier dérivé.
La dimension "énergie" du lagrangien est ainsi mise en évidence pour la mécanique.
Pour les autres systèmes, soumis à des interactions, la notion de force généralisée doit être précisée.
Ainsi ceux soumis à des forces dérivant d'une "énergie potentielle" seront analysés dans le paragraphe qui suit.
