Pour finir ce chapitre sur la même note que le précédent, légèrement décalée par rapport à la mécanique, la propriété de jauge du lagrangien est appliquée à la description d'une particule dans un champ électromagnétique.
Cette propriété met en évidence le rôle particulier de la vitesse, une des familles de variables généralisées prédominantes du formalisme lagrangien, et présente dans cette interaction.
La transformation de jauge permet le passage entre deux lagrangiens décrivant deux systèmes selon :
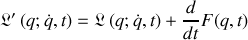
où
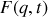est la génératrice de la transformation : sa forme permet de construire un ensemble de systèmes évoluant selon le même schéma.
Démonstration :
Ces deux lagrangiens décrivent le même comportement physique.
En effet si
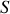et
sont les actions de chacun des lagrangiens,
Après intégration de la seconde intégrale, l'expression suivante est déduite :
La fonction
est évaluée aux instants
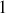et
:
, instants pour lesquels
.
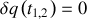La trajectoire qui minimise
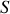va donc minimiser
puisque :
.
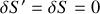La physique des systèmes décrit par l'un ou l'autre des lagrangiens sera donc la même.
L'expression de la fonction n'est pas encore définie.
Mais cette propriété sera valide pour toute fonction
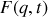, définissant ainsi une famille de lagrangiens porteurs de la même description physique.
Trois remarques sont à pointer :
1) Bien que décrivant les mêmes évolutions, la forme des deux lagrangiens n'est cependant pas identique puisque si pour le premier système :
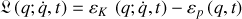, le second s'écrit :
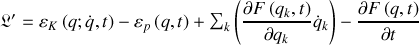
Les équation d'Euler Lagrange du lagrangien le plus simple pourront être analysées.
2) Le terme proportionnel à la vitesse peut être écrit :
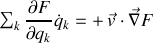
Cette forme d'un produit scalaire généralisé entre la vitesse et un champ vectoriel local, élaboré à partir du gradient de la fonction génératrice, est valide si les coordonnées sont cartésiennes.
3) Réunissant d'un coté, ce qui est fonction des vitesses généralisées et de l'autre, ce qui l'est des coordonnées généralisées, la forme suivante permet de passer d'un lagrangien à l'autre :
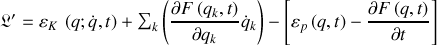
en utilisant des transformations induites par la jauge sur les lagrangiens.
Le lagrangien qui suit s'inspire de la différence introduite par la propriété de jauge. Il présente une particularité.
Attention : Un lagrangien invariant de forme.
Le lagrangien suivant est construit par extension, dans l'espace réel :
Il comporte deux champs locaux : l'un, scalaire, décrit l'énergie potentielle habituelle, et le second, vectoriel et non conservatif, est proportionnel à la vitesse.
Ce lagrangien est conforme au formalisme de Lagrange et au principe de moindre action.
À partir de ce lagrangien, toute transformation de jauge produira un lagrangien du même type (invariant de forme) :
Il suffira d'effectuer les remplacements suivants, réunissant notamment les termes dépendant ou non des vitesses selon :
et
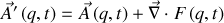
Les interactions permises par la nature sont celles décrites par la forme lagrangienne ci-dessus.
Ainsi en est il des interactions électromagnétiques, dérivées dans l'exemple qui suit.
Pour le vérifier, il faut remonter aux forces générant un tel lagrangien.
Exemple : Jauge et interaction électromagnétique
Dans l'espace à trois dimensions, le lagrangien décrivant une particule de masse
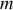évoluant dans ce champ est exprimé selon :
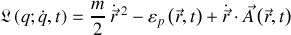
Il permet de déduire les 3 équations d'Euler Lagrange suivantes, une par composante
:
soit en notations vectorielles :
de sorte qu'avec les définitions suivantes :
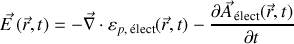
et
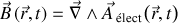
champs électrique et magnétique sont retrouvés.
Et l'équation différentielle décrivant le mouvement de la particule sera :
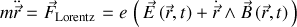
À la charge près, les grandeurs 'potentiels électriques scalaire et vectoriel' sont identifiées et la force de Lorentz reconstituée.
L'invariance de jauge lagrangienne peut être également comparée à celle de Coulomb en électromagnétisme puisque les équations de Maxwell sont invariantes si les transferts suivants sont effectués :
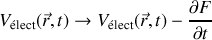
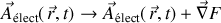
Si
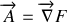aucun nouveau champ n'est généré par la transformation, autre que le champ électromagnétique de départ : aucune interaction nouvelle n'est apportée et décrite par la jauge.
Par ailleurs, la condition
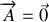permet de décrire l'interaction électrique ou gravitationnelle.
La physique décrite par l'interaction électromagnétique n'est pas donc affectée par la transformation de jauge.
L'axiome suivant :
"la nature physique est telle qu'observée : invariante de jauge "
peut être compris selon
"l'immuable réalité expérimentale de la nature se modélise par l'invariance de jauge".
