L'élaboration de la fonction de Lagrange s'établit donc par classes de cas.
Une grande famille de problèmes, dont un lagrangien commun peut être élaboré, est abordée ici.
Ainsi celle des systèmes fermés, définis ici au sens le plus large, par des contraintes ne dépendant pas explicitement du temps.
Cette propriété particulière associant la variable temps et les contraintes du système permet de définir un système dont les solutions sont accessibles.
Ces systèmes sont bien délimités et, à priori, n'ont aucun échange énergétique direct avec le milieu défini comme étant extérieur, via un moteur par exemple.
Si les variations d'énergies comptabilisées sont internes au système ou reliées à des travaux de forces externes et/ou de longue portée, dérivant d'une énergie potentielle, ils constituent le sous groupe le plus important des systèmes fermés : celui des systèmes conservatifs.
Certains systèmes fermés peuvent néanmoins détériorer l'énergie, par des forces de frottements aux points de contact.
Le traitement lagrangien de ces forces fait apparaître le rôle particulier de la vitesse généralisée.
Finalement quelques systèmes non fermés au sens énergétique comme la tige tournant à vitesse angulaire constante (et donc utilisant l'apport d'un moteur) sont néanmoins décrits par le formalisme lagrangien.
La contrainte extérieure apportée par le moteur consiste en une forme holonome (et rhéonôme puisque dépendant du temps
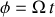) et intégrable, permettant de réduire le nombre de degrés de liberté sans réduire la portée du formalisme.
Outre ces situations déjà spécifiques, un exemple est développé en signe de généralité du formalisme lagrangien.
La particule chargée dans un champ électromagnétique est décrite par un lagrangien construit sur des arguments de jauge et d'invariance de forme.
Le rôle de la vitesse généralisée sera encore une fois souligné.
La méthode utilisée dans ce chapitre est la suivante :
L'objectif premier est d'exprimer la dynamique d'un système à
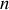degrés de liberté soumis uniquement à des forces qui travaillent et essentiellement extérieures.
Une méthode générale est déduite du principe de d'Alembert ou principe des travaux virtuels pouvant intégrer toute forme de force répertoriée.
Cependant même si les systèmes physiques sont soumis à de nombreuses forces, certaines d'entre elles ne travaillent pas, comme les forces de liaison.
L'idée de départ est donc d'évaluer le travail de toutes les forces et d'imaginer un déplacement pour lequel la somme des travaux de ces forces se compensent : c'est la notion de travail virtuel et de déplacement virtuel qui le sous tend.
De cette formulation du travail, s'exprimant dans l'espace réel, l'étape suivante la plus importante est le transfert du travail entre l'espace réel et celui des coordonnées généralisées.
Il permettra alors
de définir, le plus généralement possible, les notions d'accélération et de force généralisées,
puis de les appliquer aux différentes classes de problèmes pour aboutir à une forme utilisable des équations d'Euler Lagrange.
