La forme la plus générale de la force généralisée sera dérivée en premier avant d'être appliquée aux forces dérivant d'une énergie potentielle puis au cas du frottement visqueux.
Méthode : Traitement général
Les forces généralisées peuvent se décliner en deux cas de figures :
les forces conservatives pour lesquelles une forme lagrangienne unique existe mettant en jeu leur particularité (l'énergie potentielle),
les forces non conservatives pour lesquelles aucune méthode systématique ne peut être construite.
Le cas particulier de la force de friction proportionnelle à la vitesse (frottement visqueux typique de basses vitesses et d'écoulement laminaire) pour laquelle une forme d'énergie potentielle pourra néanmoins être établie.
Mais quel que soit le type de force considéré, la force généralisée s'écrit sous la forme suivante :
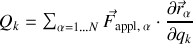
Cette forme va être adaptée aux différents types de forces et de systèmes.
Remarque :
L'écriture ci dessus correspond à un problème à N corps, notés
.
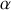Cependant pour simplifier l'écriture mais aussi à des fins pédagogiques, le cas à N corps sera évité, permettant ainsi de mettre l'accent sur les phénomènes de base et leur compréhension.
Le retour à la généralisation à N corps sera construite aisément par la suite :
en identifiant au moyen du paramètre
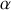des grandeurs relatives aux particules,et en effectuant une sommation discrète sur
.
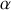Attention : Signification de la force généralisée
Cette expression de la force généralisée met en jeu un produit scalaire entre deux vecteurs : la force réelle et une variation relative, celle de la position induite par chacune des coordonnées généralisées.
Ce produit scalaire, entre force et déplacement de chaque particule, ne fait intervenir que les forces qui travaillent : celles non perpendiculaires aux déplacements.
En termes de dimension, si la coordonnée généralisée est une distance, la force généralisée a une dimension de force (en Newton).
Si
est un angle, le rapport des variations exprime un déplacement par unité d'angle, la force généralisée représente un couple ou un moment. Multipliée par un angle, elle permet également de mettre en jeu un travail.
La résultante de forces appliquées est quelconque.
Dans le cas général, la force généralisée est calculée, si possible, par composante active
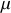selon la forme ci dessous :
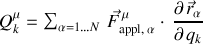
puisque chaque force appliquée est une résultante de forces.
Chaque composante apparaît de façon additive au second membre de l'égalité selon
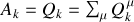, de sorte que :
Cette équation reste à décliner selon les cas de forces présentes dans le système, notamment celui non conservatif du frottement dissipatif de type visqueux.
La généralité des forces conservatives permet le développement exact et caractéristique qui suit.
Système conservatif
Les forces dérivent d'une énergie potentielle.
Elles sont de deux types : à longue portée ou forces de champ, et à point d'application comme la force de rappel qui sera traitée dans l'exemple.
Les forces à longue portée (électrique ou gravitation)
s'appliquent sur toutes les particules repérées par leurs positions dans l'espace et indicées par
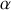, dérivent d'énergies potentielles, indicées
pour préciser le type et notées
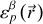dans ce qui suit.
Ainsi :
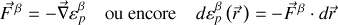
décrit la relation entre force et énergie potentielle de type
, qui s'exercent en tout point de l'espace où se trouve la particule.
Par définition, l'énergie potentielle ne dépend que des coordonnées généralisées (et non des vitesses généralisées).
En effet si la forme de
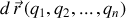est développée selon les variations des coordonnées généralisées :
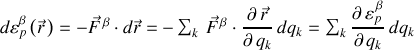
La dernière expression est obtenue par identification directe et en appliquant les lois de passage de l'espace réel à l'espace des coordonnées généralisées.
La force généralisée issue de chaque énergie potentielle, et relative à l'ordre
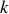, s'écrit :
.
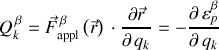L'énergie potentielle totale est la somme des énergies potentielles, quelle que soit leur origine, tout comme la résultante des forces appliquées est la somme de toutes les forces.
Il en est de même pour les forces généralisées.
Le théorème des travaux virtuels pour un système conservatif se décline sous la forme :
Cette expression est générale pour tout système conservatif ; elle est équivalente, notamment, au second principe de Newton.
Par définition, l'énergie potentielle ne dépend que de la position des particules, et non de leurs vitesses.
La transformation vers les coordonnées généralisées sous contraintes holonomes maintient cette dépendance, uniquement en
, de sorte que les équations précédentes se transforment légèrement.
Fondamental : Équations d'Euler-Lagrange d'un système conservatif
Les équations décrivant le mouvement d'un système conservatif sont :
.
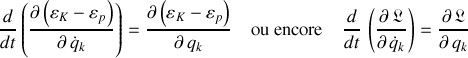où la fonction de Lagrange du système ne dépend pas du temps, comme ce sera explicité plus loin.
Elle s'écrit :
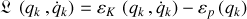
Les équations différentielles dérivées pour le lagrangien sont les équations d'Euler - Lagrange du mouvement.
Une application directe des équations d'Euler Lagrange est présentée dans le cas d'un ressort.
Exemple : Énergie potentielle élastique.
Selon le schéma choisi, il s'agit d'une force de rappel s'exerçant à l'extrémité d'un ressort et sur un point matériel,
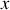ou
.
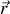La forme générale de la force généralisée s'exprime en fonction de l'énergie potentielle élastique au point d'application
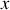ou
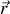, pour une oscillation
ou plus.
Les constantes de raideur peuvent être différentiées ou non, selon la direction.
Ainsi dans le cas
, l'énergie potentielle s'écrit :
alors que l'énergie cinétique est celle des coordonnées cartésiennes d'une particule de masse
.
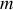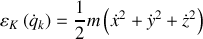
Les équations d'Euler Lagrange produisent trois équations du second degré, indépendantes, pour chaque direction, et ayant chacune sa propre force de rappel, donc sa propre pulsation.
Les conditions initiales peuvent introduire des déphasages entre les oscillations selon les trois directions, pouvant entraîner de belles figures de Lissajous.
Le cas plus complexe de vibrations des molécules autour de leurs positions d'équilibre, dues à des liaisons dipolaires par exemple, n'est qu'une généralisation de cette force de rappel (et de l'énergie potentielle élastique) précédente.
Elle s'applique au CDM de chaque molécule de masse
.
Le système de molécules peut alors être discret ou continu, et les points d'application des forces sont rapportés aux centres de liaison.
Une somme discrète ou une intégrale sur la position des liaisons (ou molécules) s'ajoute à l'expression ci-dessus.
Et surtout des couplages via l'énergie potentielle apparaissent puisque une particule qui se déplace selon
, par exemple, est soumise au rappel de toutes ses voisines.
Les molécules alignées sont un exemple d'initiation pour le passage du discret au continu, par exemple.
Remarque :
Par analogie avec les équations de Newton, et au vu de
la forme particulière de la fonctionnelle et
- de la dépendance de l'énergie potentielle en
, et les contributions en forces dont celles dérivant des énergies potentielles sont déduites du membre de droite.
Le membre de gauche peut être assimilé à la variation au cours du temps d'une quantité de mouvement, d'où la définition suivante.
Définition : Impulsion généralisée et moment conjugué.
L'impulsion généralisée ou moment conjugué associé à la coordonnée généralisée
est définie par :
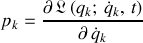
Cette grandeur est à comparer à la vitesse généralisée
.
Remarque : Impulsion, quantité de mouvement, moment conjugué
L'impulsion généralisée est une grandeur dont la signification sera explicitée au fur et à mesure de son utilisation et qui jouera un rôle fondamental dans le formalisme canonique de Hamilton.
De fait, dès la mécanique classique et au cours d'un déplacement, le sens physique est contenu non pas dans la vitesse mais dans la quantité de mouvement.
Lorsque la résultante des forces appliquées est nulle, c'est la quantité de mouvement totale qui est conservée et non pas la vitesse seule.
Ceci parait évident lors de chocs ou collisions, mettant en jeu plusieurs corps.
De même dans les situations décrivant des rotations, c'est le moment cinétique qui peut être conservée et non pas la vitesse angulaire.
Et la notion d'inertie est sous-jacente, portée par la masse ou ... le moment d'inertie. (voir le grain 1)
Frottement visqueux. Fonction de Rayleigh
Comme toutes les forces ne dérivent pas d’une énergie potentielle, la forme générale des équations d'Euler-Lagrange qui en tient compte est la suivante :
Les forces généralisées
sont déduites des expressions générales selon le même schéma que pour les forces conservatives :
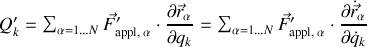
La propriété, dérivée précédemment et introduisant une dérivée temporelle au numérateur et dénominateur de la variation relative, a été utilisée.
Cette dernière formulation des équations d'Euler-Lagrange permet ainsi de tenir compte de certaines forces identifiées, notamment celles dépendant de la vitesse du mouvement.
Les forces de dissipation, non conservatives et proportionnelles à la vitesse comme le frottement (friction) visqueux, en font partie.
Le rôle particulier de la vitesse, dans le formalisme lagrangien, apparaît ainsi dans la définition d'une "énergie particulière".
Ces forces sont exprimées de façon empirique sous la forme :
où, selon l'impact du frottement expérimental, la puissance peut augmenter avec l'amplitude de la vitesse.
Le coefficient de proportionnalité peut être vectoriel pour décrire des frictions différentiées selon les
directions de l'espace.
Le frottement visqueux correspond à
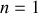, et pour de faibles vitesses.
Si la force dissipative est notée en coordonnées scalaires :
où les composantes
.
Cette expression reportée dans la force généralisée produit la forme suivante :
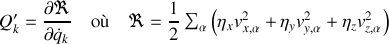
est la fonction de Rayleigh.
Les frottements ont toujours lieu dans la direction du mouvement (et à contre-sens).
Leur travail de dissipation de l'énergie est donc incontournable.
Ce n'est pas le cas de certaines forces de contact, comme les réactions des supports toujours perpendiculaires aux surfaces de contact, ou de certaines forces de liaison issues de contrainte ou même de certaines forces d'inertie.
Si elles sont perpendiculaires aux déplacements des éléments étudiés, leur travail s'annule.
Cette propriété apparaît dans la formulation générale de la force généralisée... dans le produit scalaire avec le déplacement virtuel ou réel.
Ainsi le formalisme lagrangien est un formalisme énergétique, et scalaire, mais de plus n'interviennent et ne contribuent que les forces qui travaillent dans l'espace réel.
