Dans l'espace réel, chaque particule
est repérée par
et chacune par ses trois composantes.
Le passage aux coordonnées généralisées peut s'effectuer car les relations
sont supposées connues.
Méthode : Espace réel , espace généralisé.
Chaque déplacement virtuel infinitésimal s'effectuant pendant
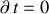s'écrit en fonction des variables généralisées :
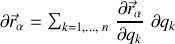
annulant ainsi la contribution d'une dépendance explicite en temps.
Pour appliquer le principe des travaux virtuels, le principe fondamental de la dynamique (second principe de Newton) constitue l'armature du calcul.
L'évaluation des travaux pour chaque élément du système s'écrit :
Le formalisme lagrangien consiste à exprimer les travaux ci-dessus en fonction des variables généralisées, soit formellement :
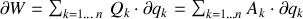
Cette forme définit les forces et accélérations généralisées, respectivement
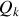et
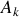, des grandeurs devenues scalaires et non plus vectorielles.
Le passage du vectoriel au scalaire s'effectue aisément en exprimant les déplacements virtuels en fonction des coordonnées généralisées, selon la formule ci-dessus, puis en permutant les sommations.
Fondamental :
Les forces
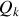et les accélérations
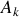généralisées sont définies par :
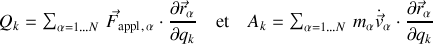
où la somme porte sur toutes les particules.
Chaque expression est constituée de produits scalaires entre vecteurs.
Après passage aux grandeurs généralisées, la formulation du théorème des travaux virtuels s'écrit simplement selon :
Ceci correspond à
relations indépendantes, les coordonnées généralisées étant des variables indépendantes.
Le résultat qui précède est général.
Mais à ce niveau, le lagrangien n'est toujours pas construit.
Les forces généralisées se déclineront en fonction du système considéré, nécessitant un traitement au cas par cas.
Par contre les accélérations généralisées présentent, quant à elles, des dérivées de vitesse susceptibles d'être associées à une énergie cinétique et donc à une forme plus globale et générale.
Elle sera donc traitée en premier.
