Le lecteur pourra vérifier (en cartésiennes par exemple) que la divergence d'un rotationnel est toujours nulle. Par conséquent, vu que

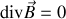
il est tentant d'écrire, en analogie avec le champ électrique

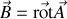
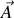est appelé potentiel vecteur. Il est déterminé à une constante vectorielle près (un gradient, puisque le rotationnel d'un gradient est nul) de même que le potentiel électrique est déterminé à une constante près qui disparaît lorsqu'on en prend le gradient.

Nous verrons, de façon réciproque, qu'en électrostatique

Figure 24 : Tube de lignes de champ magnétique de section variable

Figure 25 : Lignes de champ magnétique d'un barreau aimanté, matérialisées par de la poudre d'oxyde de fer (ferrite)

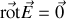
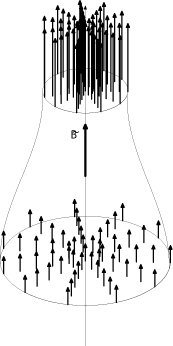
et que c'est pour cette raison qu'on peut écrire

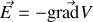
En reprenant la forme locale du théorème d'Ampère nous obtenons de même comme

et

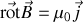
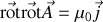
or si nous nous souvenons que

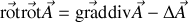
vu le choix de constante que nous avons, nous pouvons prendre une constante telle que 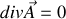(choix dit jauge de Coulomb) et donc finalement

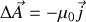
équation de Poisson qui relie le potentiel à ses causes.

Rappelons que pour le potentiel électrique nous avions

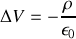
et que d'autre part le potentiel est également relié à ses sources par la loi de Coulomb

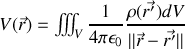
par analogie, pour chaque composante de 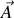nous obtenons une équation similaire reliant le potentiel vecteur à ses sources

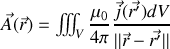
et en prenant le rotationnel de cette dernière expression nous retombons sur la loi de Biot et Savart, ce qui nous rassure à la fois sur la cohérence interne de l'électromagnétisme classique et sur nos capacités en calcul. Remarquons que la démonstration sans analogie nécessite des connaissances nettement plus avancées en mathématiques (théorie des distributions).

On peut remarquer que 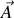est obtenu directement à partir de ses causes (sans produit vectoriel) et donc qu'il est un "vrai" vecteur, intrinsèque, contravariant et donc qu'il est contenu dans les plans de symétrie de ses causes et orthogonal aux plans d'antisymétrie de ses causes. Rappelons cependant que son expression dépendra du choix de jauge (car il est défini à un gradient près) et du référentiel choisi car 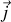est proportionnel à la vitesse relative des charges par rapport à l'origine des coordonnées (usuellement on se place dans le référentiel du laboratoire supposé galiléen).