Vous aurez peut-être remarqué que jusqu'à présent nous n'avons fait qu'un usage modéré des outils mathématiques présentés dans la première partie du cours. Nous allons y remédier en reprenant les théorèmes de Gauss et d'Ampère et en introduisant les densités de charges et de courants : ainsi pour le théorème de Gauss

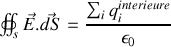
se transforme en

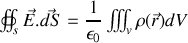
en remplaçant encore une fois les charges ponctuelles par leur densité moyenne sur un élément de volume 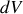et en sommant sur le volume 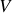enserré par la surface 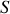et contenant les charges (strictement, sans charges sur la surface).

De même pour le théorème d'Ampère

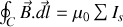
devient

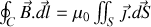
en sommant sur la surface enserrée par .

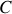Nous souvenant des formules de Green-Ostrogradski et de Stokes, il nous vient alors une forte envie de transformer le membre de gauche de ces expressions pour obtenir

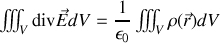
et

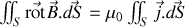
Comme les volumes 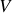ou les surfaces 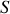sont quelconques, en les rendant infiniment petites nous nous rendons compte qu'il faut que les intégrandes soit égales à gauche et à droite des deux équations. On obtient donc la forme dite locale du théorème de Gauss

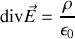
et la forme locale du théorème d'Ampère

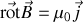
Nous verrons dans un chapitre ultérieur que cette expression n'est valable qu'en magnéto-statique et doit être corrigée lorsque les courants ne sont pas stationnaires (équation de Maxwell-Ampère).

En tout cas ces expressions sont particulièrement intéressantes car elles relient directement les champs à leurs sources, et comme annoncé dans la première partie du cours on voit que le champ électrique diverge autour de ses sources, et que le champ magnétique tourne autour de ses sources ; c'est particulièrement flagrant dans le cas respectivement d'une charge quasi-ponctuelle, on d'un fil infini parcouru par un courant (règle du tire-bouchon ou du bonhomme d'Ampère par exemple).