Désormais équipés aussi bien des outils d'intégration que de dérivation des champs vectoriels, nous pouvons envisager des relations entre ces différents opérateurs (un peu comme pour la formule de l'intégration par parties).
Par exemple si nous considérons une surface fermée
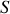enserrant un volume
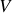on peut établir la formule suivante (formule de Green-Ostrogradski) pour un champ vectoriel
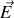(typiquement le champ électrique)
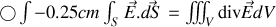
Remarquons que l'homogénéité vectorielle est respectée, de même que l'homogénéité dimensionnelle (une dérivée a la dimension de la grandeur divisée par une distance). Ce n'est pas une preuve de la formule mais c'est encourageant !
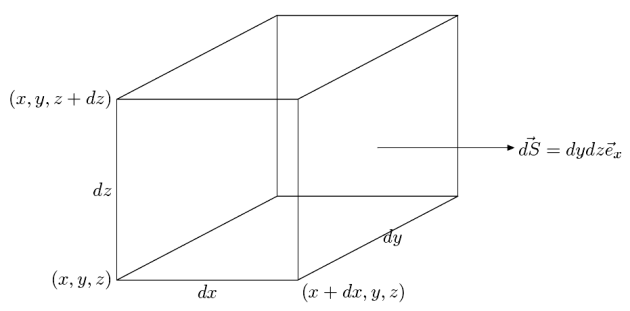
Les physiciens ont l'habitude de "démontrer" la formule de la façon suivante : d'abord, en décomposant le volume
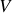en petits cubes élémentaires
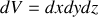de surface
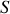. Ensuite en prenant le membre de droite de la formule
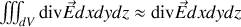
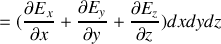
pour le membre de gauche
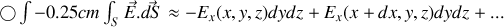
en sommant sur les six faces du petit cube, en respectant l'orientation, (normales sortantes), et en se limitant au premier ordre
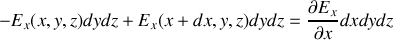
On voit donc en répétant la procédure pour
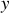et
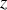que localement les membres de gauche et de droite des formules sont égaux.
En sommant sur l'ensemble du volume
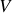étudié, il ne reste finalement que les faces extérieures des petits cubes
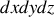et on obtient bien la formule dite de Green-Ostrogradski.
Cette formule nous sera utile pour établir la forme locale du théorème de Gauss.
