Si nous faisons désormais intervenir le potentiel électrique 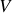, nous obtenons l'équation suivante : si nous posons

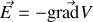
comme nous venons de montrer que

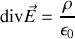
alors

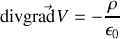
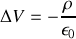
Cette équation est dite équation de Poisson et elle relie le potentiel à ses sources. C'est cette équation qui est employée en pratique sur ordinateur pour déterminer des potentiels dans des situations arbitraires (accélérateur de particules, four micro-ondes, molécules complexes...).

Dans le cas où la charge est nulle (dans le vide par exemple) on obtient l'équation dite de Laplace

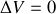
Cette équation apparaît souvent dans d'autres sous-disciplines de la physique (thermique, etc). La plupart du temps elle permet de prévoir une dépendance linéaire du potentiel dans le vide pour raccorder deux conditions aux limites : cas des condensateurs par exemple.

En effet à une dimension on obtient

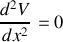
donc

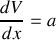
avec 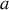une constante (correspondant au champ électrique) ; puis

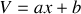
avec 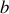une autre constante à déterminer en fonction de conditions aux limites.