Jusqu'à présent, nous avons envisagé des champs soit présents dans le vide, soit créés par des distributions de charge dans le vide, indépendamment de toute considération sur des milieux matériels, considérations repoussées dans un cours ultérieur. Cependant nombre de problèmes (autour des condensateurs en particulier pour l'électrostatique, traversée de surfaces des bobines en magnéto-statique) font appel à la traversée d'interfaces entre deux milieux matériels.

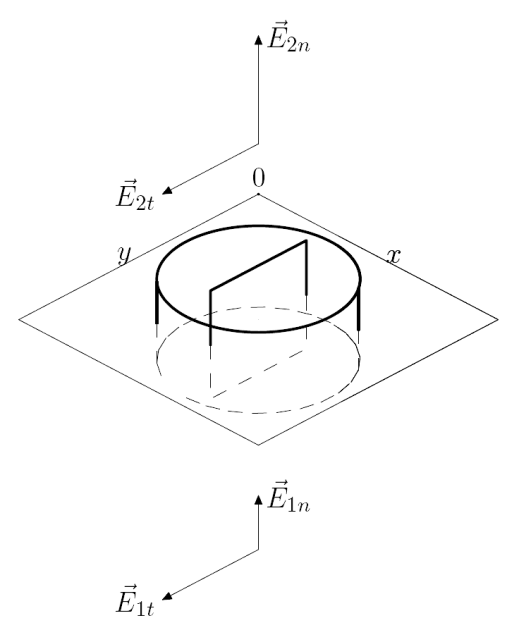
Ainsi nous allons considérer une interface localement plane séparant deux milieux matériels 1 et 2, dans lesquels nous supposerons les lois de l'électromagnétisme dans le vide inchangées. L'interface sera prise par commodité comme le plan 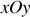. Nous supposerons que l'interface porte une charge surfacique 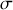et un courant surfacique 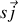mais qu'il n'y a pas de charges volumiques.

En effet, dans un conducteur parfait la densité de charges est nulle car si nous supposons valable la forme locale de la loi d'Ohm

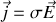
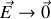si pour que le produit reste fini il faut que . Comme la forme locale du théorème de Gauss nous dit que

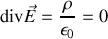
il faut que la densité de charges 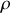soit nulle. Physiquement cela veut dire que comme les charges de même signe (électrons) se repoussent, s'il n'y a pas de force de friction, elles vont toutes partir en surface pour éventuellement former une densité de charges 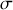s'il n'y a pas de moyen de les évacuer du conducteur.

Cette hypothèse du conducteur parfait n'est cependant pas indispensable pour la suite mais nous nous en servirons à l'occasion.

Pour une fois nous allons employer la formule de Stokes pour le champ électrique et celle de Green-Ostrogradski pour le champ magnétique.

Figure : Surface et parcours autour de la surface chargée séparant deux milieux employés pour la démonstration du théorème de Coulomb

En effet nous avons vu que le rotationnel de 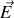est nul (du moins en régime permanent) par conséquent si nous considérons un parcours rectangulaire 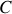coupé en deux par la surface et symétrique, de côté 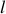et de faible épaisseur e suivant la direction 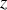, alors une application de la formule de Stokes donne

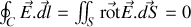
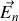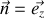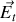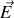Si maintenant nous détaillons la circulation, en décomposant le champ électrique dans chaque zone 1 et 2 suivant deux composantes, l'une en projection sur la normale à la surface, et l'autre dite composante tangentielle composée de la projection de ce vecteur suivant une direction donnée perpendiculaire à la normale, par exemple , alors la circulation de vaut

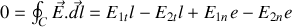
si nous choisissons le parcours rectangulaire tel qu'il soit colinéaire à .

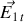Par conséquent en faisant tendre l'épaisseur 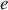vers 0 on a continuité de la composante tangentielle à la traversée de l'interface. Cela sera vrai également si nous considérons la direction 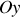, et donc vrai pour l'ensemble de la partie du champ contenu dans le plan.

Si maintenant nous appliquons le théorème de Gauss à une boîte cylindrique (ou "camembertoïdale") de surface 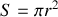et d'épaisseur e faible, également coupée en deux par l'interface, alors comme

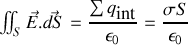
et que l'intégrale surfacique s'approche par

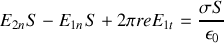
puisque nous avons vu que la composante tangentielle était continue. Si maintenant nous faisons tendre l'épaisseur 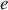vers 0, il reste après simplification par

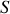
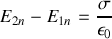
résultat que l'on nomme parfois théorème de Coulomb et que l'on peut résumer (avec la continuité de la composante tangentielle incluse) en

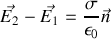
De la même façon pour le champ magnétique, en employant le fait que sa divergence est toujours nulle, puis avec le théorème d'Ampère, on peut établir a contrario que sa composante normale est continue alors qu'on a une discontinuité de la composante tangentielle, résultat dont la démonstration est tout à fait similaire résumé par

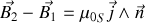
Par exemple à la traversée de la surface d'un solénoïde créant un champ magnétique constant en son sein, et nul à l'extérieur, on a une discontinuité exactement donnée par l'expression ci-dessus.