Le principe de Curie qui stipule pour tout phénomène que la symétrie des effets est un sous-ensemble de la symétrie des causes peut nous guider pour ce faire.
La dépendance spatiale des valeurs des champs électriques ou magnétiques sera donc obtenue par les symétries de leurs causes, respectivement charges et courants. Par exemple si le courant parcourt uniformément un fil cylindrique supposé infini d'axe
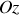suivant ce même axe, alors le champ magnétique, en coordonnées cylindriques ne dépendra ni de
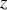ni de l'angle polaire
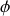vu l'invariance des causes par translation ou rotation et donc éventuellement seulement de la distance
à l'axe.
Pour la direction des champs électriques ou magnétiques, la situation est légèrement différente. En effet comme le champ électrique est un "vrai" vecteur (dit aussi contravariant), correspondant à un effet physique intrinsèque qui doit être le même dans tous les systèmes de coordonnées et quelle que soit l'orientation de l'espace, on peut montrer que ce champ électrique doit être contenu dans les plans de symétrie de ses causes et orthogonal au plan d'antisymétrie de ses causes.
Par contre, le champ magnétique dépendant du choix de l'orientation de l'espace, il est dit covariant, ou axial, et on montre qu'il est contenu dans les plans d'antisymétrie de ses causes et orthogonal aux plans de symétries de ses causes.
Ainsi, lorsqu'on calcule l'effet physique des champs sous la forme de force de Lorentz, dans les deux cas (électrique ou magnétique) la force, qui elle est intrinsèque, aura la même valeur et orientation après application des éléments de symétrie des causes.
Par exemple considérons une surface chargée d'une densité de charges telle que
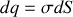, de faible épaisseur, contenue dans le plan
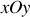, et de dimension infinie. Tout plan orthogonal à
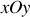st manifestement un plan de symétrie des causes du champ électrique, et le champ électrique doit donc être contenu dans ce plan ; le champ électrique est donc orienté suivant
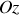et les forces subies par une éventuelle charge
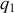auront la même direction et finalement présenteront la même symétrie que les charges. Si nous considérons une charge
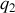symétrique de
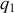par rapport au plan
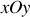celle-ci subit une force
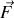symétrique de la précédente.
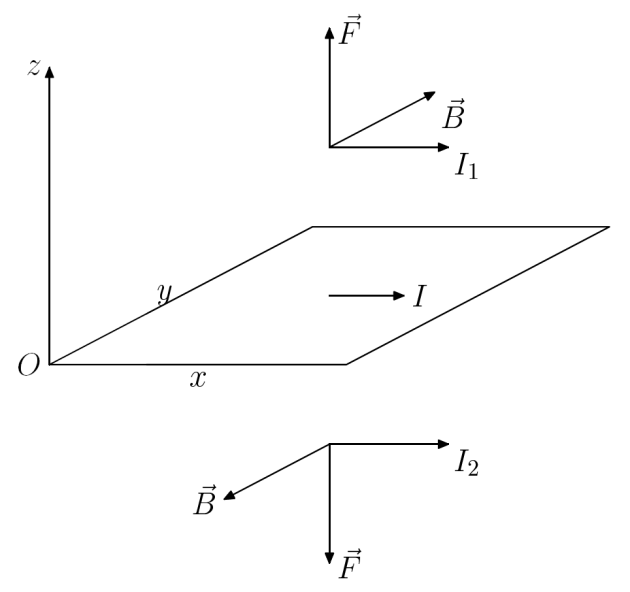
Si maintenant nous considérons dans les mêmes conditions une nappe de courant contenue dans le plan
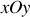et un courant
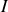coulant dans la direction
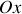par exemple, le plan
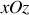est plan de symétrie donc le champ magnétique lui sera orthogonal, et le plan
est plan d'antisymétrie donc le champ sera contenu à l'intérieur. On peut donc prévoir une direction suivant
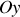pour le champ magnétique ; si maintenant nous considérons un fil électrique parallèle à
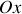à une certaine distance du plan parcouru par une intensité
celui ci va subir une force de Laplace
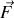suivant
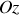qui présentera bien les symétries planes des courants. Si maintenant nous considérons un fil parcouru par un courant
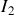symétrique de
par rapport au plan
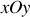, le champ magnétique change de sens sur ce fil, ainsi que la force de Laplace qui a un sens conforme à l'intuition (deux fils parcourus par des courants parallèles se repoussent).
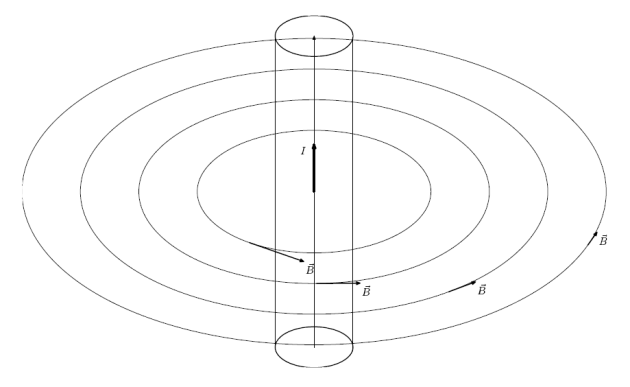
Ces considérations de symétries nous permettront en anticipant la forme des lignes de courant (les lignes sur lesquelles les champs ne varient pas) de choisir de façon pertinente les surfaces ou les parcours pour l'application des théorèmes de Gauss ou d'Ampère. Par exemple dans le cas d'un fil infini cylindrique parcouru par un courant uniforme
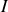suivant
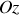, nous avons prévu que le champ magnétique ne dépendrait que de
; en outre les considérations de symétrie nous permettent de prévoir que le champ sera orthogonal aux plans de symétrie de ses causes, à savoir tout plan contenant le fil ; le champ sera donc orthoradial (suivant
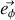et les lignes de courant seront des cercles centrés sur l'axe du fil et orthogonaux à celui-ci. Nous prendrons donc dans le théorème d'Ampère un parcours constitué d'un cercle de rayon
et nous pouvons sortir le champ de l'intégrale vu qu'à
donné le champ est constant, et à l'extérieur du fil on aura
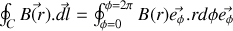
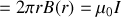
et finalement
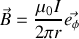
Remarquons qu'à l'intérieur du fil le résultat serait différent car le membre de droite ne serait pas constant ; ce calcul intéressant est laissé en exercice.
