Nous avons dit dans les paragraphes précédents que les lois de Coulomb et de Biot et Savart étaient peu adaptées au calcul de champs dans des situations non-standard. Il existe en effet des formulations indirectes des relations de cause à effet dues à Gauss (pour la gravitation, mais celle-ci est formellement équivalente à l'électrostatique) et à Ampère qui sont bien plus pratiques. Ces relations démontrées dans les premiers cours d'électromagnétisme en remarquant que la définition des angles solides fait intervenir un terme en inverse du carré de la distance apparaissant dans les lois de Coulomb ou de Biot et Savart sont les suivantes : si nous considérons un volume 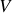enserré par une surface 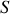fermée, et que ce volume 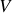contient (à l'exclusion de sa surface) un ensemble de charges 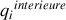, alors le flux du champ électrique créé par les charges sur la surface 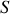est proportionnel à la charge totale présente dans le volume 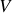. Le théorème de Gauss se formule alors

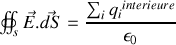
Le facteur 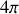présent dans la loi de Coulomb disparaissant lors de l'intégration sur tous les angles solides. Il est à noter que ce théorème étant très simple, certains physiciens en particulier anglo-saxons vont jusqu'à poser 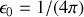(unités de Gauss).

De même pour le champ magnétique si nous considérons une courbe fermée 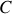enserrant une surface 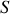alors la circulation du champ magnétique le long de la courbe 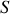est proportionnelle à la somme des courants traversant la surface

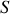
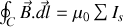
Là encore le facteur 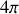disparaît. En unités de Gauss par contre on prend 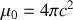avec 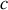célérité de la lumière.

On voit que les théorèmes de Gauss et d'Ampère peuvent nous permettre de calculer facilement les champs créés par des distributions quelconques de charges ou de courants à condition de choisir une surface ou un parcours d'intégration simple (typiquement, une sphère, un cercle, ou un cube et un carré). Les symétries du problème peuvent nous y aider.