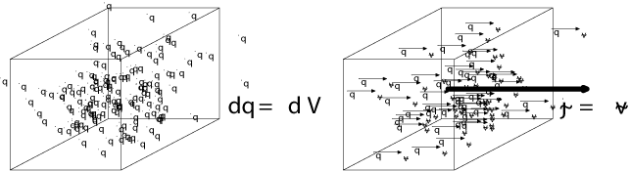
On peut passer d'une distribution de charges discrètes 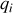dans l'espace (correspondant typiquement à des noyaux chargés positivement et aux électrons négatifs les entourant) à une distribution continue de charges 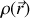en moyennant sur un petit volume 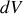, petit face aux dimensions d'un problème typique étudié mais grand face aux dimensions atomiques.

Alors la charge 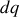contenue dans le petit volume vaudra

Figure 15 : Distribution de charges ponctuelles en mouvement créant une densité continue de charges et de courants

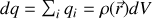
avec 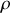la densité de charges, champ scalaire dépendant de la position. Ce champ est tout à fait analogue à une densité ou masse volumique dépendant de la position et moyennant sur les masses des atomes.

De même, si les charges sont en mouvement avec une vitesse 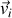, on définit le courant élémentaire comme

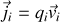
et la densité de courant dans le petit volume par

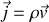
où 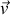est la vitesse moyenne des charges .

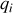En principe il faudrait de plus sommer sur toutes les espèces de porteurs de charges présentes (ions et électrons). En physique nous nous limiterons au cas de charges constituées d'électrons uniquement, sauf dans les problèmes traitant de plasmas.

Ces distributions de charges ou de courants peuvent être quasi-mono-dimensionnelles (cas d'un fil mince), quasi-bidimensionnelles (cas d'une surface mince). Dans ces cas on aura intérêt à définir des densités de charges ou de courants linéiques ou surfaciques, en intégrant sur les dimensions non pertinentes. Ainsi on définit la densité de charges 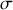d'une surface en écrivant que

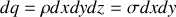
en supposant que la surface est mince suivant la direction 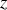et ne présente pas de variations intéressantes de densité.

De même on définit la densité de charges linéiques 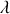pour un fil

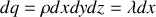
en supposant que les seules variations sont suivant 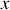, la densité surfacique de courant 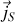par

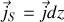
en supposant qu'il n'y a pas de variation suivant 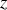et que la surface est mince.