Ces définitions vont permettre de donner plusieurs expressions des lois de Coulomb et Biot et Savart reliant les champs à leurs causes.

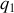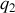En effet Coulomb a montré au dix-huitième siècle par des expériences très délicates et inspirées par la théorie newtonienne de la gravitation que la force attractive ou répulsive entre deux charges électriques et (exercée par la première sur la seconde) situées en 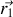et 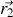respectivement était proportionnelle au produit algébrique de celles-ci, était alignée sur l'axe les reliant, et variait en inverse du carré de leur distance suivant

Figure 18 : Force de Coulomb entre deux charges ponctuelles

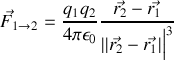
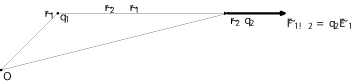
Une distance sur le cube d'une distance est bien homogène au carré d'une distance, et cette formule exprime de façon concise l'axe de la force. On vérifie bien que deux charges identiques se repoussent et que deux charges identiques s'attirent. Le coefficient de proportionnalité, très proche de 9.10⁹ en unités du système international (ce qui n'est pas anodin comme nous le verrons dans le dernier chapitre) est exprimé en fonction de la "perméabilité du vide" 0.

On définit alors le champ électrique 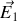créé par la première charge et tel que

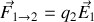
Remarquons que ce champ varie lui aussi en carré de la distance. Il est traditionnellement exprimé en volts par mètre car si nous introduisons le potentiel électrique 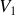créé par la charge tel que

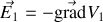
on retrouve bien cette dimensionnalité. Le potentiel 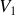vaut alors

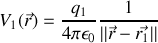
et il varie en inverse de la distance à l'origine de la charge.

Les champs et potentiels électriques obéissent au principe de superposition, ce qui veut dire que le champ ou potentiel total créé par une distribution de charges 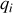situées aux positions 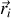valent au point 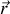respectivement

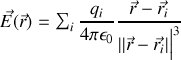
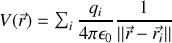
Si maintenant nous passons à une distribution continue de charges, il suffit de remplacer (par une procédure mathématique non détaillée ici) les sommes par des intégrales et les charges par des densités volumiques 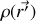situées au point 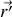de la zone de volume 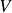où sont les charges, multipliées par des éléments de volume et on obtient

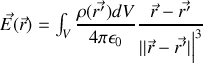
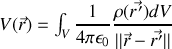
On peut montrer en prenant le rotationnel de cette expression que 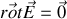, point sur lequel nous reviendrons.

En ce qui concerne le champ magnétique, la situation est quasiment identique à celle du champ électrique. Le magnétisme, connu depuis l'invention de la boussole par les Chinois, et étudié en Europe depuis la Renaissance (par Gilbert par exemple), était considéré un phénomène indépendant de l'électricité jusqu'à ce que, peu après l'invention de la pile électrique par Volta permettant d'obtenir de bien plus fortes intensités que celles obtenues par les machines électrostatiques du type Wimshurst, le Danois Oersted remarque par suite du désordre régnant sur son bureau qu'un courant électrique pouvait faire dévier l'aiguille d'une boussole.

Ampère et Biot et Savart, après communication de cette information révolutionnaire pour l'époque, ont alors établi les lois quantitatives de la magnéto-statique.

La loi de Biot et Savart permet de relier les causes du champ magnétique 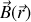en un point de l'espace à sa valeur. Ainsi de façon analogue à la loi de Coulomb on a

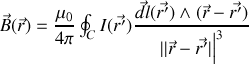
L'intégration se faisant sur les circuits forcément fermés parcourus par des courants 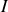dépendant de l'espace mais non du temps (état stationnaire mais hors d'équilibre).

On retrouve ici le produit vectoriel dont nous parlions dans les paragraphes précédents et qui implique que le choix d'orientation de l'espace influe sur le signe du résultat.

On peut déduire de ce résultat que 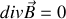, point sur lequel nous reviendrons.

En pratique, les lois de Coulomb et de Biot et Savart sont rarement employées, que ce soit dans les exercices "scolaires" ou en pratique sur ordinateur par exemple, sauf dans des cas très simples (distributions linéiques droites ou circulaires de charges et de

Figure 19 : Boucle de courant créant un champ magnétique

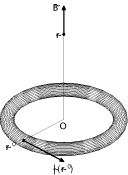
courants) car elles nécessitent une intégration compliquée géométriquement et analytiquement pour chaque point considéré dans l'espace. Elles ont cependant l'avantage de relier directement les causes aux effets.