Toujours faire des figures claires et employant des couleurs. Éviter les cas particuliers dans les figures (30 degrés, 45 degrés...)

Raisonner le plus possible en français clair, introduire les équations seulement lorsqu'elles sont nécessaires, éviter les abréviations et les quantificateurs d'existence.

Partir d'un rappel du cours pertinent en définissant bien les hypothèses employées (symétries, est-on dans le vide, linéarités...)

Lier les étapes du raisonnement par des mots-clefs (or, donc, mais, puisque...) commenter les résultats obtenus (sens de variations, cas limites) pour voir si l'on retrouve des cas connus ou évidents. Estimer de tête à partir des puissances de 10 les ordres de grandeur des applications numériques et commenter les résultats s'ils sont surprenants, faire attention aux unités (tout résultat doit en avoir une, même "SI"), tout remettre en SI (en particulier les cm, mA, Celsius, calories etc) et vérifier l'homogénéité des résultats (ne pas "additionner moutons et chèvres", ne pas prendre le logarithme ou le sinus de quantités dimensionnées). Un correcteur acceptera plus facilement une erreur algébrique dans les coefficients qu'un résultat non homogène du point de vue des unités ou pire un résultat non homogène vectoriellement ( .....)
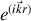