L'entropie 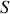est une fonction d'état du système considéré. Dans le cas d'un système fermé divariant, c'est une fonction de deux paramètres d'état. Choisissons par exemple les paramètres (énergie interne) et (volume) qui sont, comme 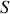, extensifs (doublant lorsque l'on réunit deux systèmes identiques) :

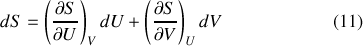
Notons que les dérivées partielles de l'entropie sont ici des grandeurs intensives, en tant que rapports de grandeurs extensives. Considérons maintenant le problème simple d'une interaction thermique quasi-statique entre deux systèmes A et B séparés par une cloison rigide et diatherme, l'ensemble étant isolé du reste de l'Univers.

Initialement, les deux systèmes ne sont pas en équilibre thermique. Du fait que la paroi est diatherme, un échange thermique a lieu entre A et B jusqu'à ce que l'équilibre soit atteint. La paroi étant rigide, les volumes de A et B restent invariants et la différentielle de l'entropie, somme des différentielles des entropies de A et B, ne dépend que des variations différentielles des énergies internes de A et B.

De plus, le système A+B est isolé. Son énergie interne est constante et la différentielle de cette énergie interne reste nulle à toutes les étapes de la transformation. Par suite, la différentielle de l'énergie interne de B reste l'exacte opposée de celle de A.

À l'équilibre thermique enfin, d'après le second principe pour un système isolé, l'entropie est à son maximum. Aussi la différentielle de l'entropie de A+B et n'importe laquelle de ses dérivées partielles sont nulles, en particulier la dérivée partielle de 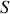par rapport à l'énergie interne de A. Cela implique l'égalité :

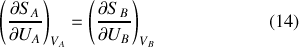
Or, l'équilibre thermique est également défini par une égalité des températures des deux systèmes A et B. La grandeur intensive que constitue la dérivée partielle de l'entropie par rapport à l'énergie interne est donc en relation avec la température.

Dans la mesure où il faut construire une fonction 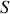encore inconnue, il est possible d'identifier cette dérivée partielle avec une expression de la température, ou plutôt de son inverse puisque l'énergie a une dimension proportionnelle à celle de la température.

Cette dernière égalité constitue une définition mathématique de la température thermodynamique du système considéré. L'entropie acquiert ainsi la dimension de la constante 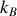de Boltzmann .
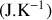