Le système A+B isolé du reste de l'Univers est à nouveau considéré, avec cette différence que la cloison diatherme qui sépare A et B est devenue mobile. Les volumes
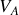 et
et
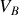 de ces deux sous-systèmes peuvent maintenant varier au même titre que les températures
de ces deux sous-systèmes peuvent maintenant varier au même titre que les températures
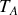 et
et
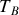 ou les pressions
ou les pressions
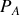 et
et
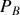 .
.
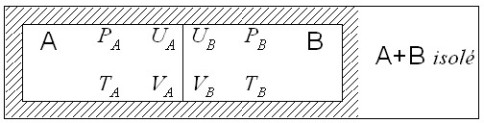
C'est donc une interaction thermique et mécanique qui se produit à partir de l'état de déséquilibre initial entre A et B. Cependant, le système A+B restant isolé et de volume constant,

L'expression de la différentielle de l'entropie totale peut donc être donnée au cours de la transformation sous la forme :
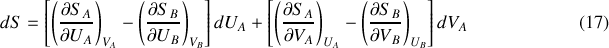
Lorsque l'équilibre est atteint, les températures thermodynamiques étant égales, la différentielle de l'entropie totale et sa dérivée partielle par rapport au volume
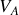 étant nulles, il vient :
étant nulles, il vient :
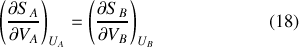
Or, ces dérivées partielles ont la dimension du rapport d'une pression à une température,
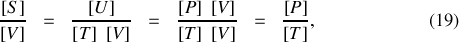
tandis qu'à l'équilibre mécanique et thermique les pressions et températures de A et B se sont égalisées :

Une définition simple de la dérivée partielle de
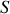 par rapport à
par rapport à
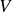 peut donc être :
peut donc être :

La différentielle
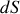 acquiert ainsi la forme générale :
acquiert ainsi la forme générale :
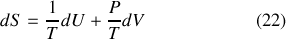
Ce qui est nommé Relation thermodynamique fondamentale en découle directement :
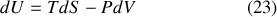
Le second terme du second membre de la relation (23) correspond au travail différentiel
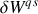 échangé au cours d'une transformation quasi-statique. D'après le premier principe, le premier terme correspond donc au transfert thermique différentiel
échangé au cours d'une transformation quasi-statique. D'après le premier principe, le premier terme correspond donc au transfert thermique différentiel
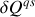 réalisé au cours d'une telle transformation. Par identification, il apparaît que la relation thermodynamique fondamentale contient les deux principes de la thermodynamique à condition de poser :
réalisé au cours d'une telle transformation. Par identification, il apparaît que la relation thermodynamique fondamentale contient les deux principes de la thermodynamique à condition de poser :

C'est là une définition différentielle de l'entropie et du second principe.
Remarque :
la relation thermodynamique fondamentale a été déduite de l'étude de l'interaction thermique et mécanique entre deux systèmes fermés. D'autres échanges d'énergie, liés à l'ouverture des systèmes ou de nature chimique, peuvent intervenir. Ils sont abordés ultérieurement ;
dans le rapport
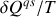 , la température thermodynamique
, la température thermodynamique
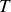 est celle du système dont on considère l'entropie
est celle du système dont on considère l'entropie
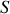 , pas celle du monde extérieur avec lequel le système interagit ;
, pas celle du monde extérieur avec lequel le système interagit ;l'expression (24) peut être utilisée pour calculer le long d'un chemin quasi-statique la variation d'entropie du système entre deux états d'équilibre, même si la transformation qui conduit de l'état initial à l'état final n'est pas quasi-statique. En effet, la variation de la fonction d'état
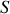 ne dépend pas du chemin suivi. Toutefois, il faut souligner que la nature de la transformation quasi-statique qui conduirait au même état final serait différente de la transformation réelle. On verra plus loin qu'une transformation adiabatique non quasi-statique s'accompagne d'une augmentation d'entropie du système thermiquement isolé. Ce n'est donc pas une transformation quasi-statique adiabatique qui pourrait lui être équivalente, mais une transformation quasi-statique au cours de laquelle le système recevrait de l'énergie par chaleur du monde extérieur.
ne dépend pas du chemin suivi. Toutefois, il faut souligner que la nature de la transformation quasi-statique qui conduirait au même état final serait différente de la transformation réelle. On verra plus loin qu'une transformation adiabatique non quasi-statique s'accompagne d'une augmentation d'entropie du système thermiquement isolé. Ce n'est donc pas une transformation quasi-statique adiabatique qui pourrait lui être équivalente, mais une transformation quasi-statique au cours de laquelle le système recevrait de l'énergie par chaleur du monde extérieur.




