Imaginons que le sous-système A précédemment considéré soit un gaz parfait, le sous-système B restant quelconque. La fonction d'état entropie de A doit vérifier l'égalité de Schwarz :

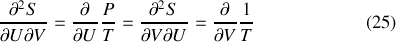
Il s'agit en réalité d'une condition sur la température thermodynamique 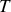. Or, cette condition est vérifiée dès lors qu'on identifie la température thermodynamique de A à la température du gaz parfait. En effet pour un gaz parfait, l'énergie interne ne dépend que la température (1^ère Loi de Joule) et :

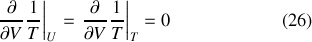
Par ailleurs, en raison de la Loi des gaz parfaits,

et il est aisé de montrer que l'autre dérivée mixte de l'entropie du gaz parfait est également nulle :

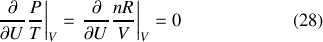
L'égalité de Schwarz étant ici vérifiée, il n'y a pas lieu de faire la distinction entre température thermodynamique (ou absolue) et température du gaz parfait. La température thermodynamique d'un système quelconque comme B peut être définie par la température du gaz parfait qui serait en équilibre thermique avec lui.