Introduction
Du plus simple au plus compliqué et partant des acquis associés au point matériel, le solide indéformable (rigide) est un système de points matériels indénombrables situés à des distances fixes les uns par rapport aux autres.
Ainsi cette définition comporte une approximation : à l'échelle de l'étude, les changements de forme et de dimensions sont négligés.
Pour dériver les équations du mouvement d'un solide, le mouvement général sera décomposé en deux :
une vue globale d'un ensemble (rapporté à un point matériel) en translation dans l'espace et
un
« zoom »
plus précis sur le mouvement relatif constitué uniquement de rotations autour d'axes associés au solide.
Chacune de ces sous descriptions nécessite une représentation et des outils.
Complément : Solide et degrés de liberté
Pour rappel, le nombre
de degrés de liberté d'un système est obtenu en déterminant
le nombre
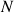de particules du système et le nombre
de contraintes.
Pour un mouvement dans l'espace à
dimensions, ce nombre vaut :
Quelques exemples significatifs
Pour décrire le mouvement d'une tige filiforme, le suivi de deux points de la tige (donc équidistants ce qui constitue la contrainte) suffisent et
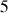degrés de liberté (donc
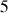variables indépendantes) sont nécessaires : trois pour le mouvement global et deux rotations. Des
variables nécessaires pour décrire un solide, une troisième rotation, autour de l'axe de la tige, disparaît avec l'absence de points hors de la tige.
Pour décrire un plan, il faut également
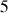variables spatiales. En effet lorsque
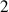particules fixes du plan sont repérées (
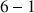degrés de liberté), la troisième l'est automatiquement (relation d'Al Kashi, ou Pythagore généralisé, dans un triangle quelconque) ; cette propriété définit
points quelconques d'un plan.
Ainsi dans les deux cas ci-dessus,
coordonnées repèrent le CDM (ou un point particulier du solide), et seules deux rotations subsistent pour des raisons de symétrie.
Une particularité du plan : les
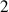axes contenus dans le plan sont interchangeables ce qui réduit le nombre de rotations.
Ainsi en termes de degrés de liberté, le solide comporte
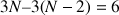degrés de liberté en vertu des nombres de coordonnées et de contraintes constituées par les distances entre particules. Au delà de
particules, la particule additive a toujours
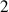proches voisines dans l'espace.
Sur les
degrés de liberté du solide, idéalement
trois vont être affectés à la translation du centre de masse (CDM) ou de n'importe quel point fixé au solide et
les trois restants pour le mouvement relatif autour de ce point.
Ces
derniers degrés de liberté décrivent le mouvement du solide indépendamment de sa translation dans l'espace. Ils s'exprimeront dans un référentiel d'axes fixes et fixé au solide. Ce dernier ne peut alors effectuer que des mouvements affectant de la même manière tous les points du solide : des rotations.
De plus, dans le cas le plus général le solide effectue
rotations par rapport à
axes du solide qui resteront à définir.
Par opposition avec ce qui précède et en présence de solide déformable, les changements de forme ne sont plus négligeables.
Devient alors nécessaire un traitement point par point caractérisé par sa complexité.
S'il est possible, un traitement par groupe de points, partageant les mêmes propriétés, peut s'inspirer de la démarche développée pour le solide.
En effet ces propriétés apparaissent sous forme de contraintes.
Pour exemple de solides déformables,
la chaîne ou la corde dont la distance entre deux éléments est constante, deux par deux (points ou blocs de points) mais dont la direction (la rigidité) ne l'est pas forcément...
Cet exemple est partiellement traité dans le cours sur le formalisme lagrangien.
Le système le plus général de
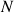points en interaction est régi par
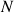équations vectorielles.
Cependant et quel que soit le type de solide indéformable, la description des deux types de mouvement nécessite au moins deux référentiels "fixes" :
si la translation globale d'un point du solide est exprimée dans un référentiel fixe, celui du laboratoire par exemple, et nécessite la position d'un point de référence,
les rotations du solide et surtout les axes autour desquels elles vont avoir lieu, ne peuvent être appréhendés sans une meilleure connaissance du solide et sa position initiale.
Ces deux remarques conduisent à la nécessité d'identifier les points et axes de référence d'un solide.
Et pour cela, il est utile de se déterminer sur le traitement des
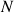points du solide.
