Approche descriptive du solide : du discret au continu
Partant de la représentation du point matériel, le solide est un ensemble discret de points matériels mais tellement proches, qu'indéformable ou non, il peut être considéré comme continu du point de vue macroscopique.
Ainsi toutes les sommes discrètes qui apparaîtront dans le traitement du solide pourront être transformées en intégrales sur la structure solide : une intégrale simple ou surfacique ou volumique selon le solide.
Exemple : La masse : du discret au continu
Pour obtenir la masse d'un solide constituée de
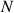particules élémentaires de masses
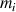une sommation discrète du type
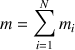est nécessaire.
L'approximation continue consiste à considérer une distribution de masse par unité de longueur, de surface ou de volume.
Pour une distribution sur un volume, la masse volumique est notée
(
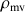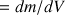). Elle peut être constante ou non, selon l'homogénéité du solide.
La masse élémentaire
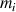devient l'élément de masse
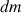et s'écrit
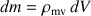pour un volume.La sommation discrète se transforme alors en intégrale simple pour une distribution linéique (
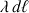), double pour une surface (
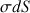) et triple pour un volume.
L'intégrale porte alors sur toute la ligne de masse, la surface ou le volume du solide selon l'objet de l'étude, soit :
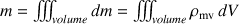, pour un volume.
Toutes les démonstrations de ce cours seront développées en utilisant la sommation discrète.
La règle développée dans l'exemple ci-dessus s'appliquera aux situations concrètes, aux applications.
Ainsi en est il de la détermination du centre de masse (CDM) du solide, défini par ses coordonnées dans un repère orthonormé fixe de centre
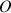par:
,
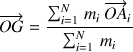mais également des grandeurs physiques utiles pour l'étude du mouvement, comme l'énergie cinétique totale ou le moment cinétique total du solide, qui appliqueront cette règle de continuité dans la matière.
