Référentiel mobile et vecteur rotation
Les positions de chaque point
du solide dans les référentiels, fixe
et mobiles
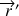, sont notées :
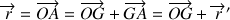
Le passage du CDM,
à un centre quelconque
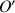est effectué selon :
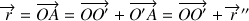
L'un ou l'autre est susceptible de décrire le mouvement global du solide : sa translation dans l'espace.
Ce sont des sommets possibles de référentiel mobile.
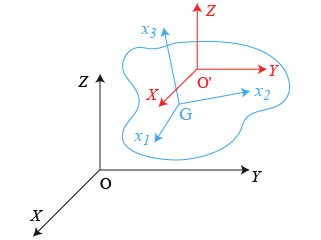
En fonction de ce choix, qu'en est-il de la rotation du solide ?
Une des spécificités de la rotation est qu'elle impacte de la même manière tous les points du solide et cela quel que soit le centre du référentiel associé au solide.
Ce qui importe, c'est l'identification des axes de rotation.
Fondamental :
Le vecteur-vitesse rotation
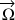est une grandeur absolue du mouvement du solide : elle est la même pour tous les points du solide quel que soit le référentiel choisi pour la description.
Dans un mouvement de rotation décrit par une phase
, la vitesse linéaire de chaque point du solide croît proportionnellement à sa distance à l'axe de rotation. La vitesse angulaire, elle, est la même pour tous les points.
Ainsi pour chaque rotation, cette vitesse est associée vectoriellement au seul axe de rotation (de direction
).
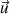Chaque point du solide, étant à distance constante de cet axe, décrit un cercle de rayon constant dans le plan perpendiculaire à l'axe avec le même vitesse angulaire
.
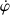Et le vecteur vitesse angulaire
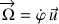permet un repérage unique de chaque point sur le cercle. (Fig. 3)
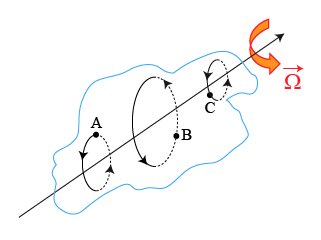
Ce vecteur rotation est-il affecté par un choix de référentiel ?
Pas par les axes du nouveau référentiel puisque la direction de la rotation est fixée : il suffit d'effectuer les projections sur les axes de référence choisis,
ni par le sommet du référentiel comme le montre la démonstration suivante.
Explication : Vitesse angulaire et référentiel
La relation de passage entre le référentiel de laboratoire et celui mobile (en rotation) lié au solide s'écrit au moyen de la composition des vitesses suivantes :
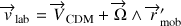
La vitesse angulaire est portée par trois axes de rotation, dans le cas général ; le centre du repère mobile, décrivant le mouvement global, est ici
, le CDM.
Autour du second repère mobile, de centre
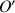appartenant au solide et tel que le vecteur
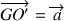est constant, la vitesse de translation du point
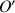est notée
.
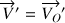La vitesse angulaire dans le nouveau repère est supposée se différencier selon
.
La vitesse dans le référentiel du laboratoire de tout point
du solide s'écrira selon le repère mobile utilisé :
où la position du point
est repérée respectivement par rapport à
puis à
.
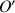L'expression suivante :
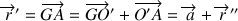
permet de passer de la première expression de la vitesse ‘absolue' à la seconde, par un simple report selon :
Ou encore :
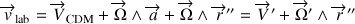
La dernière égalité reprend la vitesse du point
dans le second référentiel mobile.
Une identification terme à terme permet de déduire deux propriétés :
La vitesse de translation du référentiel mobile est tributaire du sommet choisi selon une relation bien connue :
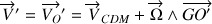
Elle exprime la composition des vitesses pour chaque point du solide, ajoutant l'effet de la rotation au mouvement du CDM.
La rotation est indépendante du centre du référentiel mobile car
Ainsi tous les points du solide ont la même vitesse angulaire, quel que soit le référentiel mobile choisi, en direction d'axes ou en sommet.
Cette démonstration conduit à deux propriétés fondamentales pour le choix du référentiel mobile.
L'une affirme le caractère absolu (et l'unicité) de la vitesse angulaire de rotation du solide.
En termes de rotations, l'important est la direction de l'axe de rotation (sa réalité) : le vecteur vitesse de rotation est porté par cet axe.
Tout choix d'axes
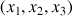induira juste une projection de cette vitesse angulaire sur les nouveaux axes.
De fait, la démonstration ci dessus n'a impliqué aucun axe d'aucun référentiel.
La seconde propriété vient de la relation liant les vitesses des centres.
Le nouveau centre du référentiel mobile voit deux contributions à sa vitesse : la translation globale, associée au centre de masse, plus un effet de la rotation.
De fait, cette relation est plus générale puisque :
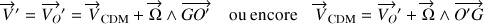
où les rôles des sommets apparaissent interchangeables, donnant lieu à un outil qui permet de simplifier la description du mouvement du solide.
La démonstration ci-dessus permet ainsi de définir la notion d'axe instantané de rotation.
Fondamental : Axe instantané de rotation
Un axe instantané de rotation est un axe dont l'ensemble des points
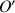est caractérisé par une vitesse instantanée nulle soit :
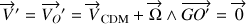
ou encore :
.
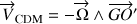Cette définition est équivalente à une condition de roulement sans glissement du solide, comme il sera vu plus loin.
Plus généralement, la condition décrivant l'axe instantané de rotation permet de lier la translation du CDM du solide à sa rotation autour de ses axes.
Les exemples qui suivent permettent de visualiser la condition.
Exemple :
Les deux cônes de la Fig. 2 ont des axes instantanés qui passe par le point fixe
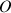et le point de contact avec le sol. Il s'agit dans les deux cas de la génératrice
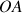.Pour un cylindre qui roule sans glisser sur un plan, incliné ou non, l'axe de rotation réel est l'axe de symétrie du cylindre : tous les points du cylindre tournent autour de cet axe qui passe par le
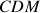. L'axe instantané est encore la génératrice du cylindre en contact avec le plan. Elle est parallèle à l'axe du cylindre.
A chaque instant, tous les points du cylindre, et du cône, semblent tourner autour de la ligne que les points de la génératrice forment : un axe momentanément figé.
L'instant d'après, une autre génératrice prend le relais dont chaque point est caractérisé par une vitesse instantanée nulle.
Ceci explique la dénomination ‘instantané'.
