Le théorème du moment cinétique
Le moment cinétique de chaque composant du solide par rapport à une origine
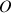, appartenant au solide, est le moment de sa quantité de mouvement.
Ainsi le moment cinétique total s'écrit :
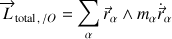
Sa dérivée temporelle s'écrit :
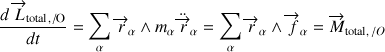
Apparaît le moment résultant de toutes les forces externes qui s'appliquent sur chaque point du solide.
Les forces internes, qui s'appliquent au même point, s'annulent deux à deux.
C'est le théorème du moment cinétique appliqué au système de points.
Remarque :
1) Lorsque les forces qui s'appliquent sur chaque élément du solide sont quelconques, le changement de centre de calcul du moment cinétique ne modifie pas le théorème.
En effet, le passage au centre de masse est effectué avec la relation de Chasles :
.
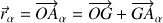Le moment des forces s'écrit :
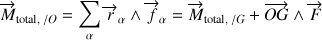
où
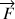est la résultante des forces.
Par ailleurs le théorème du moment cinétique total est invariant lors d'un changement de point d'application soit :
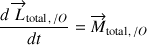
et
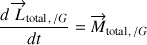
Lorsque la dérivée temporelle du moment cinétique total par rapport à l'origine
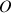est effectuée et la relation de Chasles utilisée, seules les deux contributions suivantes subsistent :
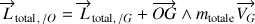
En dérivant par rapport au temps, la relation ci-dessus entre les moments de forces est retrouvée.
2) En cas de champ de forces homogène, pesanteur par exemple, le point d'application de la résultante des forces produit un moment de force nul et donc un moment cinétique local conservé.
