Rotations et formalisme lagrangien
L'énergie cinétique et l'énergie potentielle s'expriment toutes deux en fonction de variables angulaires.
Dans le cas général du solide, trois rotations peuvent être envisagées de sorte que, pour ces variables notées également
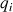par uniformité, les équations du mouvement de Lagrange s'écrivent :
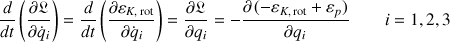
Cette équation est exacte et tient compte de toutes les contributions possibles.
Pour une rotation
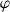de vitesse angulaire
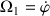, (la démonstration ci après peut être reproduite pour les autres variables angulaires, notées
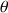et
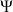par exemple) et partant de l'énergie cinétique de rotation totale qui s'écrit
,
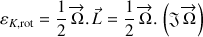l'équation du mouvement de Lagrange correspondant à
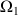est :
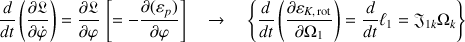
Les expressions à gauche (extérieures aux accolades) sont l'expression du principe de moindre action pour toute variable.
Entre accolades (à droite), le membre de gauche du principe (dérivée temporelle totale) est appliqué au solide et incluent toutes les composantes concernées du tenseur d'inertie.
Ainsi la généralité du formalisme lagrangien produit des contributions systématiques : le terme issu de l'énergie cinétique de rotation conduit à la variation du moment cinétique, rotation par rotation.
Le membre de droite du principe, terme dépendant de l'énergie potentielle, peut être évalué à partir du travail de la force... à l'origine de la rotation et donc associée à sa phase.
Ceci peut être obtenu en utilisant le théorème de l'énergie cinétique suivant pour chacun des constituant du solide :
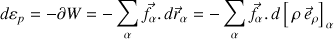
Le cas général d'un déplacement élémentaire comprenant une rotation est représenté sur les Fig. 8a et 8b.
Dans le cas général, la variation d'énergie potentielle s'écrit :
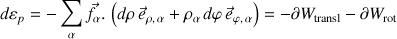
Les deux contributions obtenues concernent respectivement la translation et la rotation.
En effet, la première produit un éloignement (ou un rapprochement) par rapport au centre
,
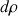indépendant du point considéré
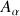du solide, alors que la seconde décrit la rotation et dépend de la position du point.
Pour un solide indéformable, le centre du repère appartient au solide et dans l'énergie cinétique de rotation, seul le déplacement
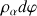est pris en compte.
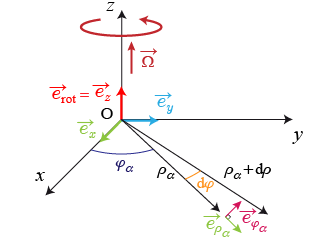
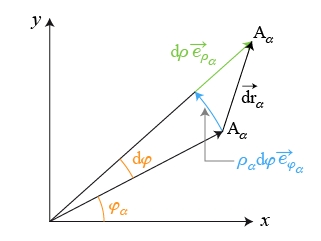
Dans le cas d'une rotation pure d'angle
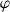autour de l'axe vertical
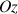, selon les notations des coordonnées polaires, la variation élémentaire du rayon vecteur est un arc
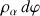porté par le vecteur unitaire
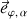tel que
.
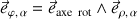La variation d'énergie potentielle est :
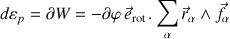
Le résultat final a été obtenu par permutation circulaire dans le produit mixte, effectuée pour en extraire la rotation et son axe, communs à tous les points du solide, et laisser ainsi paraître le moment résultant des forces
.
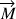En présence de plusieurs rotations, la quantité
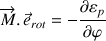n'est rien d'autre que la projection du moment de la résultante des forces sur l'axe de la rotation
.
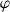Attention :
Cette projection indique que la variation temporelle de la composante du moment cinétique concernée est celle sur l'axe de rotation : elle est donc perpendiculaire au plan de la rotation. Et non pas selon la direction
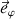bien que les dérivations lagrangiennes concernent
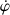et
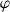.La distance
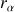ci-dessus peut dépendre d'un autre angle, comme de l'angle
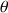dans le cas de coordonnées sphériques. Les informations portées par ce cas seront traitées plus loin.
Rappel :
En résumé, et comparativement au point matériel, pour décrire le solide quelques points émergent.
L'articulation entre le ‘mouvement du CDM' et les ‘rotations' est retranscrite en termes de ‘translation‘ et ‘rotation', bien séparées.
Ceci met en place le centre d'inertie et son rôle d'articulation permettant de déduire un ensemble d'équations estampillées selon le schéma vectoriel suivant
Un PFD appliqué au centre de masse (et d'inertie) avec un bilan des forces incluant toutes les forces extérieures au solide dont celles aux points de contact, lesquelles n'apparaissent pas dans le lagrangien.
Cette partie est similaire au mouvement du point matériel, qui en est la simplification.
Un théorème du moment cinétique qui met en jeu le moment des forces contribuant aux rotations.
Avec le formalisme lagrangien, les termes issus de variables angulaires tiennent compte de toutes les forces qui travaillent y compris celles d'inertie.
Finalement et comme pour le point matériel, le théorème de l'énergie cinétique pour les systèmes conservatifs, donc dans sa forme ‘conservation de l'énergie mécanique totale', ne peut être utilisé pour la résolution du mouvement du solde que pour une variable unique ou alors à titre de vérification.
