Théorèmes généraux et torseurs
La dérivée temporelle est appliquée au pseudo vecteur cinématique.
Ceci permet de déduire en toute généralité :
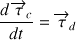
Chacun peut reconnaître dans cette formulation doublement vectorielle et symétrique, le théorème du centre d'inertie et celui du moment cinétique, obtenus tous deux en appliquant la seconde loi de Newton.
La généralisation au système de points et au solide est similaire.
Partant des définitions générales de l'impulsion totale et de son moment par rapport à un point O, le moment cinétique total selon :
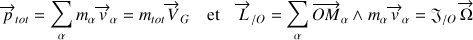
Le torseur cinématique (ou des quantités de mouvement) est établi comme suit :
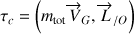
Et celui dynamique (ou des quantités d'accélération) selon :
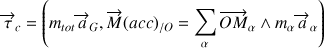
Appliquant le PFD au système de points, ce dernier torseur s'écrit :
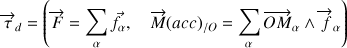
La force
est la résultante des forces qui s'appliquent sur le système de points et
la résultante de celles qui s'appliquent sur le point
.
Ainsi le second vecteur composant le torseur dynamique apparaît comme la somme de moments de toutes les forces qui s'appliquent sur chaque point du système.
Tout comme le point matériel, le torseur dynamique est la dérivée temporelle du torseur cinétique : ce qui représente une forme condensée des théorèmes du centre d'inertie et du moment cinétique.
Remarque :
Le passage du référentiel fixe de centre
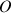à un référentiel mobile de centre
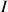, quelconque, s'effectue au moyen de la relation générale suivante pour le moment cinétique total :
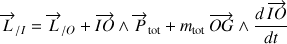
Si
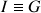le centre de masse du solide alors :
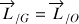
Ou encore dans le cas particulier d'un référentiel de centre
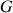
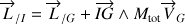
Cette relation permet de tenir compte d'un éventuel axe instantané de rotation passant par I, parallèle à l'axe de rotation passant par G.
