Pour cette première application, l'approximation du point matériel est assumée et le mouvement du pendule est considéré comme plan.
Syntaxe : Quelles variables, quels paramètres ?
Le pendule est une bille ponctuelle de masse
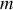et de longueur
.
Son mouvement plan est décrit par une seule variable d'espace : son inclinaison par rapport à la verticale.
Cet angle, noté
, sera la coordonnée généralisée choisie ; la vitesse généralisée est la vitesse angulaire
.
Les coordonnées polaires s'imposent (Fig. 2).
Le vecteur qui repère la position de la bille est porté par la direction radiale.
Il est noté:
.
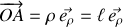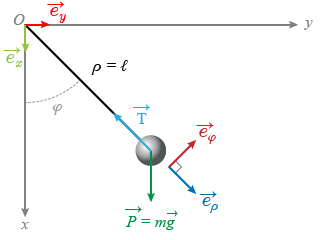
Méthode : La spécificité du pendule plan
La barre filiforme qui relie la bille à l'origine des axes a une longueur constante,
,
la vitesse linéaire est portée par la direction orthoradiale et s'écrit
.
Bien qu'inutilisée dans le formalisme lagrangien, l'accélération est donnée à titre indicatif.
Elle vaut dans ce cas :
.
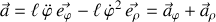Elle comporte deux composantes, respectivement orthoradiale et radiale.
Les énergies cinétique et potentielle s'écrivent respectivement :
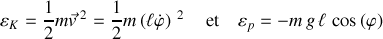
Le niveau de référence de l'énergie potentielle
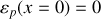est choisie à l'horizontale du point d'attache (Fig. 2).
La fonction de Lagrange s'écrit :
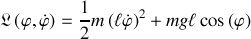
Apparaissent naturellement le couple de variables généralisées du problème
et
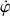, nécessaire pour dériver l'équation d'Euler-Lagrange.
Remarque : Calculs et analyses
La séparation suivante est à noter :
La dépendance en la vitesse généralisée
est toute contenue dans l'énergie cinétique, et donne lieu à une contribution d'origine inertielle.
Seule l'énergie potentielle dépend de la coordonnée généralisée
; l'énergie potentielle sera à l'origine de la force généralisée.
Une seule équation du mouvement peut être déduite, composée de deux contributions ci-dessus.
La première est déterminée par les calculs successifs :
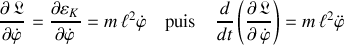
À la longueur de pendule près, la composante orthoradiale du terme d'inertie
, du second principe de Newton, est aisément identifiable.
Le second membre de l'équation d'Euler -Lagrange est aisément déduit :
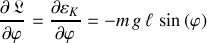
Il complète la composante orthoradiale du PFD, celle qui met en jeu la force de pesanteur.
En effet, cette composante du poids, à l'origine de l'effet de rappel (porté par le signe moins) et par conséquent du mouvement oscillant, est reconnaissable.
Mais cela toujours à la longueur du pendule près.
L'équation du mouvement obtenue par le formalisme lagrangien est identiquement :
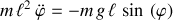
Et simplifiée par un paramètre
, cette équation n'est rien d'autre que la projection selon
) du second principe de Newton.
Ainsi le formalisme variationnel de Lagrange produit directement l'équation du mouvement du pendule.
Explication : Une équation : deux interprétations.
La présence de la longueur du pendule interpelle.
En y associant le mouvement de rotation décrit par la variable angulaire
(et l'accélération angulaire) permet de caractériser complétement l'équation différentielle obtenue.
L'équation d'Euler Lagrange ci-dessus est une application directe du théorème du moment cinétique sans sa dimension vectorielle.
Dans le membre de gauche,
le moment d'inertie de la bille
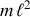apparaît avec l'accélération angulaire .
Lors de sa rotation autour de
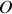, le pendule met en jeu un moment cinétique dont le module est
.
La dérivée temporelle du module du moment cinétique (impulsion généralisée) est explicitée.
Dans le membre de droite,
le moment de rappel (signe moins) du poids par rapport à l'origine des axes
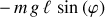y est explicite.
L'ensemble décrit bien la rotation de la masse
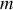autour d'un axe passant par l'origine
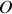du repère et perpendiculaire au plan d'oscillation.
L'équation d'Euler-Lagrange décrit l'égalité de deux vecteurs portés par l'axe de rotation.
Outre la dimension de chaque terme de l'équation et le mouvement plan, la longueur du pendule représente le vecteur position de la bille (radial) dans un produit vectoriel avec d'une part la dérivée de la quantité de mouvement de la bille et d'autre part, le poids de la bille (définition du moment de la force de pesanteur).
Le résultat de chacun de ces produits vectoriels est un vecteur perpendiculaire au plan d'oscillation : l'équation conserve l'égalité des normes dans le respect du sens trigonométrique.
Dans ce cas particulier, grandement servi par sa simplicité, l'équation d'Euler-Lagrange redonne directement la forme non vectorielle du théorème du moment cinétique.
Une simplicité qui permet de reconstituer une projection du second principe de Newton.
Méthode : Entre formalismes et images.
Cet exemple est suffisamment simple et général pour expliciter la démarche liant les notions de variable, coordonnée, vitesse ou force... généralisées, propre au formalisme lagrangien, et leurs équivalents en mécanique vectorielle classique.
Le formalisme lagrangien est, par construction, un formalisme énergétique : il ne faut donc pas en attendre des grandeurs ou expressions vectorielles... sans la démarche volontaire qui consiste à analyser la source de chaque terme.
La coordonnée généralisée (ou variable généralisée d'espace) pouvant être une distance ou un angle, en termes de norme, ce formalisme ne marque aucune différence entre les grandeurs "quantité de mouvement" et "moment cinétique ou moment de la quantité de mouvement" par exemple : toutes deux sont des impulsions généralisées.
L'une est associée à la variable généralisée "distance", l'autre à celle "angle".
En parallèle, la force généralisée est alors soit une force, soit... un moment de force, et toujours en norme active ou réactive (munie d'un signe + ou -).
Le vocabulaire sera donc plutôt réduit puisque unifié.
Les concepts également.
Le modèle lagrangien introduit une formalisation de la mécanique qui réduit la complexité à quelques images simples contenant l'essentiel de la physique.
La richesse, les détails de la mécanique classique ainsi que la dimension visuelle sont donc à reconstruire à partir des équations d'Euler -Lagrange.
Cette richesse se retrouve néanmoins complétement dans le formalisme lagrangien.
Il paraît alors possible de construire des formalismes parallèles à celui lagrangien dans d'autres domaines scientifiques : les variables généralisées étant les grandeurs décrivant le problème posé.
Les règles les régissant sont alors soit phénoménologiques et expérimentales, comme en thermodynamique, soit posées (imposées ?) comme en économie.
Attention : Choix des variables
Toute la simplicité et l'élégance du traitement précédent provient du choix des variables. Un autre choix conduit à un résultat complétement différent.
Les coordonnées cartésiennes
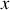et
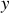peuvent également décrire le mouvement du pendule.
En effet, si la contrainte du mouvement circulaire est ignorée, l'énergie cinétique et l'énergie potentielle s'écrivent :
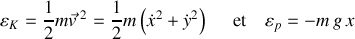
Cette description à deux degrés de liberté admet le lagrangien suivant :
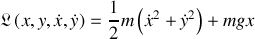
Les équations d'Euler Lagrange du mouvement s'écrivent formellement :
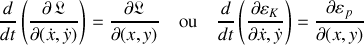
Soit lorsqu'elles sont appliquées au pendule simple :
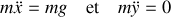
Ces équations différentielles décrivent en fait, et selon les conditions initiales, un mouvement parabolique c'est à dire un mouvement de chute libre (dans le champ de pesanteur... porté par l'énergie potentielle) dans le plan
.
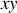Ignorer la contrainte représentée par le fil et sa tension (ou la tige rigide) et entraînant un mouvement circulaire (
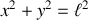) revient à considérer les deux variables comme indépendantes : ce "pendule simple" décrit en coordonnées cartésiennes a deux degrés de liberté et ne correspond pas au pendule simple réel.
La contrainte ne peut donc être ignorée dans le formalisme lagrangien du second ordre.
La notion de coordonnée généralisée associe celle de degré de liberté, de variable utile.
Utiliser les coordonnées polaires revient à choisir le système de coordonnées qui extrait aisément
la contrainte
les forces efficaces : celles qui travaillent.
Ainsi la tension du fil disparaît de la description en même temps que la variable
.
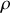La description en coordonnées cartésiennes ci-dessus peut être néanmoins corrigée en utilisant soit :
le formalisme du premier type avec la contrainte :
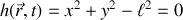pour dériver la force de contrainte, directement sur les deux équations d'Euler Lagrange ci-dessus.ou les multiplicateurs de Lagrange développés au chapitre 4.
Dans l'exemple qui suit, la bille dans une tige en rotation, l'analyse sur le nombre de degrés de liberté et le choix des variables généralisées décrivant le système continue mais avec un objectif supplémentaire : exploiter toutes les possibilités d'une situation expérimentale.
