Rappel :
Dans le cas général, ce problème traite de deux corps (de masses
et
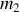) en interaction gravitationnelle ou électrostatique (charges opposées).
Il est réduit à un problème à un corps : le mouvement d'une particule fictive, de masse réduite
.
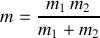Du fait de l'interaction centrale et comme dans le grain précédent, les coordonnées sphériques sont utilisées.
Le lagrangien de la particule fictive, exprimé dans le référentiel du CDM, est le suivant :
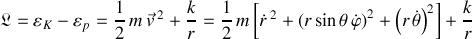
Le mouvement de la particule, sans analyse particulière préalable, utilise ainsi pleinement l'espace à
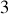dimensions.
Le système de coordonnées choisi ne permet plus la séparation des couples (énergies, variables généralisées). Et le système d'équations d'Euler Lagrange est fortement couplé.
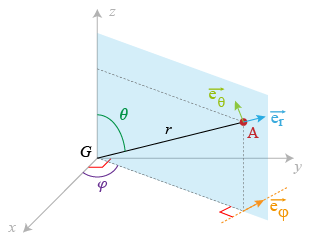
La particule fictive
est représentée sur la Fig. 7 avec les notations adoptées.
Le formalisme lagrangien permet de dériver les
équations du mouvement d'Euler- Lagrange suivantes.
Pour la variable radiale, une projection sur la direction radiale du PFD est obtenue :
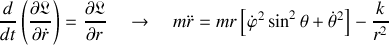
où la force d'interaction radiale est explicite.
Mais également les composantes (selon
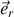, symbolisés ci-dessous par les crochets) des forces d'origine inertielle (et centrifuges) qui apparaissent du fait des deux rotations :
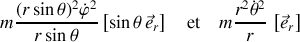
La variable angulaire
caractérise la rotation autour de l'axe vertical et son équation d'Euler Lagrange est telle que :
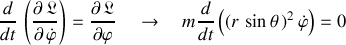
Cette équation a un sens physique : elle exprime la conservation du moment cinétique (ou angulaire) associé à la rotation
, qui s'effectue autour de l'axe fixe
.
Le bras de levier associé à la rotation (et au produit vectoriel) est :
La variable angulaire
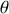caractérise la rotation autour d'un axe mobile situé dans le plan horizontal de direction
et son équation d'Euler Lagrange est telle que :
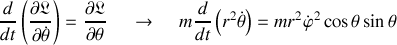
Cette équation donne la variation temporelle de la norme du moment cinétique ou moment angulaire de la rotation
.
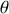Les
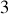équations d'Euler-Lagrange sont couplées et un moment angulaire d'axe fixe (
) est une constante du mouvement.
La rotation
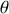a donc lieu autour de l'axe mobile
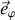situé dans le plan horizontal.
L'équation d'Euler - Lagrange relative à ce degré de liberté ne peut décrire, en l'état, la conservation du vecteur moment cinétique associé à la rotation
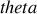.Sauf cas particulier où
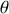est fixe et, par exemple, vaut
.
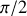Rappel :
Le moment cinétique total, somme vectorielle des deux moments cinétiques, est conservé puisque la force est centrale.
Notamment en direction et celle qui est fixe est la direction
.
La dérivée temporelle du moment cinétique relatif à
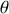produit la contribution ci-dessus, dû à la norme, et une autre dans le plan (
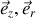). La résultante s'aligne sur la direction
.
Cette conservation permet de déduire un mouvement plan pour la particule réduite.
Dans le cas du point matériel (sans dimension intrinsèque), le mouvement plan (dans le plan de l'écliptique) ne nécessite pas l'utilisation des coordonnées sphériques : les coordonnées polaires suffisent à mener à bien la description.
Remarque : Association indirecte : le solide autour d'un centre attracteur.
Dans le grain suivant "Dynamique du solide" où sera traité le mouvement du solide, seront séparés :
le mouvement du centre de masse du système (un point matériel) s'effectuant dans le plan de l'écliptique (du CDM) lequel contient le centre attracteur, selon le schéma décrit ci-dessus, et
les rotations propres du solide autour de ses axes de symétrie, analysées dans un référentiel dont le centre est le CDM de la planète.
Ces rotations propres sont au nombre de
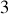: les angles ou rotations d'EULER.
Une planète, solide quasi sphérique, est en rotation autour d'un de ses axes principaux et axe de symétrie, noté
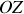(représenté par le vecteur
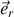sur la Fig. 7, et devenu une inclinaison de référence par rapport à laquelle chaque point du solide peut être retrouvé).
Si l'axe perpendiculaire au plan de l'écliptique du CDM, vertical, fixe et noté
, joue le rôle particulier de la direction fixe du moment cinétique total
, la conservation de
associée à la rotation de la planète autour de
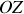autorise une inclinaison
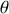de l'axe de rotation
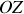par rapport à l'axe fixe
, et donc par rapport au plan de l'écliptique du CDM.
Chaque point du solide a ainsi un mouvement qui est une combinaison de deux mouvements plan : celui dans le plan de l'écliptique autour de l'attracteur et celui de rotation autour d'un axe incliné par rapport au plan de l'écliptique.
La description du mouvement du solide dans l'espace nécessite une répartition "des tâches", des niveaux d'analyse.
Au CDM la translation globale et mouvement plan en application des propriétés de la force centrale résultante, dont le point d'application sera ... le CDM.
Et au moment angulaire total, les mouvements relatifs de rotations et ici l'inclinaison de l'axe de symétrie (et axe de rotation du solide) par rapport à l'axe du moment cinétique total permettant un mouvement à trois dimensions de l'ensemble des particules du solide.
Cette inclinaison de l'axe de rotation permettra notamment d'expliquer les phénomènes de précession
et de nutation
des planètes.
Toute toupie symétrique présente ces phénomènes.
Rappel : Entre formalismes
Dans le grain précédent " Lois de Newton et référentiels. Lois de conservation", dans la partie traitant de la conservation de l'énergie mécanique totale, ce même exemple avait conduit à une composition des trois équations déduites ci-dessus par l'application directe de la théorie lagrangienne.
Ce qui précède a permis de formuler de manière simple quelques problèmes de mécanique mais également d'entrevoir les possibilités d'interprétation.
Ainsi une représentation différenciée des exemples a été entrevue, caractérisée par une convergence vers une solution unique : un problème est d'abord une traduction d'énoncé, d'hypothèses, dans un langage approprié... dans un formalisme.
