Syntaxe : L'additivité dans le formalisme lagrangien
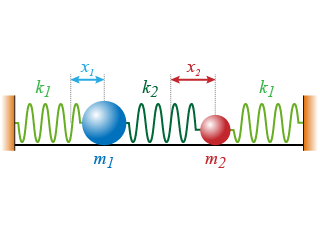
Le mouvement d'un système à deux corps est ici considéré.
Il est constitué de deux oscillateurs, deux masses ponctuelles
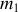et
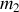, reliées entre elles par un ressort de constante de raideur
et chacune à un mur par un ressort
comme représenté sur la Fig. 4.
La configuration symétrique a donc été adoptée.
La simplicité du formalisme provient de l'additivité des grandeurs qui composent le lagrangien, et autour des deux masses.
Le nombre de masses peut être multiplié, en appliquant les mêmes règles.
À l'infini, pour aboutir au système continu ;
dans le cas ci-dessus, le système est linéaire et peut décrire, par exemple, le mouvement d'une chaîne d'atomes chargés autour de leurs positions d'équilibre.
Règle 1 :
L'énergie cinétique du système constitué par les deux masses est la somme des énergies cinétiques de chaque masse.
Elle s'écrit :
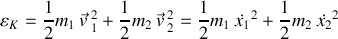
Règle 2 :
L'énergie potentielle, quant à elle, est portée par les ressorts : ce sont des énergies potentielles élastiques.
En l'absence de frottements, l'énergie potentielle est la somme de celle portée par chaque ressort (comprimé et/ou étiré ou les deux pour le ressort central) au cours du mouvement selon :
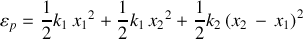
Les coordonnées généralisées
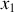et
sont algébriques : ainsi tous les cas de figures de chaque ressort, étiré ou comprimé, sont pris en compte.
La séparation des couples (coordonnées généralisées, énergie potentielle) et (vitesses généralisées, énergie cinétique) ajoute à la simplicité des équations du formalisme.
En effet le lagrangien,
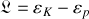, permet d'obtenir les deux équations du mouvement suivantes :
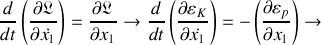
et :
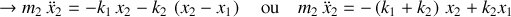
Deux notations sont présentées :
la première met en évidence les forces de rappel en jeu sur chaque masse et ainsi, les sources des contributions dans une application directe du second postulat de Newton,
la seconde, par des regroupements, pointe une piste de résolution possible.
En effet, il est utile d'identifier les changements de variables, les pulsations propres, car le système obtenu est linéaire et couplé.
La solution générale pour le couple de variables
est
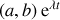où la grandeur
caractérise les fréquences d'oscillation ou modes propres (au moins deux) et où
et
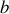dépendent des conditions initiales.
L'existence d'une solution non nulle (excluant la solution triviale) conduit à une équation caractéristique bicarrée pour
,
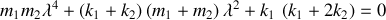
dont les solutions sont les pulsations des « modes propres ».
La mise en forme suivante permet de visualiser, sur un cas simple, l'allure générale des solutions :
où
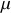est la masse réduite
.
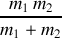Les paramètres sans dimension :
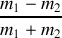et
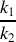, mesurent les dissymétries en masse et en constantes de raideur.
Le couple d'équations différentielles est linéaire ; la solution générale sera donc une combinaison linéaire des solutions oscillantes aux deux pulsations
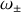(ou
).
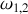Dans le cas général de deux masses quelconques, les 2 pulsations existent toujours (selon ce qui précède et
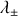) et fonction des masses témoins.
La description ci-dessus reste valide.
Exemple : Un cas particulier, les masses égales.
Ce cas permet une visualisation simple des mouvements possibles.
Quand les 2 masses sont égales, alors
et une symétrie partielle (en masse) apparaît.
Une séparation des équations peut être réalisée au moyen d'un changement de variables.
Les deux pulsations propres s'écrivent:
1)
, où l'effet du ressort central disparaît complétement. Cette pulsation est associée à la variable :
2)
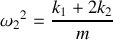où, au contraire, le ressort central est doublement actif et correspondant à une variable différence (ou variable relative) :
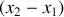
La solution générale du système linéaire est une combinaison (linéaire) de ces deux mouvements oscillants.
La première pulsation indique un mouvement régi par le seul ressort de constante de raideur
, ignorant le ressort central. Le calcul du vecteur propre, associé à cette pulsation, indique un couple de solutions
de même signe et proportionnel à
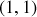, indiquant par là que les deux masses oscillent de façon symétrique (en parallèle et toujours dans le même sens).Dans ce cas, le ressort central n'intervient pas dans le mouvement des masses.
C'est le mode propre (ou mode normal) symétrique.
La seconde pulsation marque un double effet de rappel du ressort central indiquant, à l'opposé, un mouvement antisymétrique des masses et proportionnel à
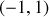, ou
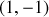selon la phase initiale.Oscillant en sens opposées l'une par rapport à l'autre, les signes de
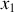et
sont opposés et le ressort central est doublement sollicité, étiré ou comprimé des deux cotés en même temps.
Le calcul des vecteurs propres conforte cette analyse.
Syntaxe : Mode propre, mode normal
La dénomination mode propre et/ou mode normal vient de la propriété suivante de ces familles de solutions : si initialement le système des 2 masses est lâché en position symétrique ou asymétrique, le système va rester indéfiniment sur le mode initial.
Ceci est une signature de stabilité et d'états de base, d'états primaires.
Si par contre, les positions initiales des deux masses sont dans des écartements quelconques, la solution générale est construite selon une combinaison linéaire des deux états décrits ci-dessus : une composition sur une base constituée de ces deux états.
Une propriété des systèmes d'équations linéaires.
