Méthode : Pré-analyse
C'est un système complexe qui peut être traité de différentes manières. (Fig. 5)
Comme l'exemple précédent, il met en jeu deux mobiles : le point matériel et le plan incliné.
Le mouvement du point matériel sur son support est non galiléen : son glissement sur le plan incliné est uniquement dû à son poids mais ce mouvement entraîne le recul du support.
La liaison entre les deux mouvements s'effectue par le biais des forces de contact.
Pour traiter cet exemple, l'utilisation en premier du principe fondamental de la dynamique, dans sa complexité, met en évidence l'élégance du formalisme lagrangien. (voir complément)
Par ailleurs et à chaque élément de résultat, le cas simple du plan incliné fixe sert de repère.
L'approximation du point matériel permet de suivre le mouvement du cube de la Fig. 5 uniquement par celui de son centre de masse
.
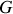Une situation, un peu plus complexe encore, met en jeu une sphère ou un cylindre roulant sur le plan incliné.
Pour cela quelques notions de mécanique du solide, portant notamment sur l'expression de l'énergie cinétique (voir l'exercice initial du chapitre VI) sont nécessaires. (voir le grain 3)
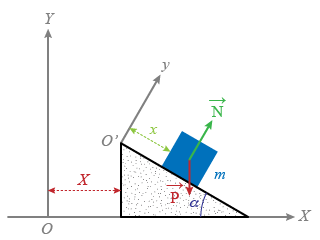
L'inclinaison du plan est fixe et notée
. (Fig. 5)
Puisque deux mouvements rectilignes (des centres de masses, du cube et du plan incliné) sont en jeu, deux degrés de liberté sont nécessaires à la description :
Le point matériel, de masse
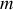, est repéré sur le plan incliné par sa coordonnée relative
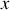, dans le référentiel mobile lié au plan incliné
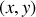, alors que
le mouvement de ce dernier, de masse
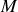, est repéré par sa coordonnée
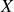, exprimée dans le référentiel fixe
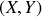. Ce mouvement produit un entraînement pour le point matériel.
Comme pour l'exercice d'application précédent, l'énergie cinétique totale des 2 corps mobiles est la somme de celle de chacun selon :
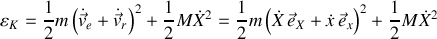
Cette expression, une fois développée, permet d'écrire l'énergie cinétique sous la forme :
ou encore :
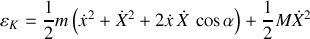
L'énergie potentielle totale est uniquement représentée par celle de pesanteur du point matériel, à l'origine de tous les mouvements.
Ainsi
où
est la hauteur du point de départ du point matériel sur le plan incliné et
, l'inclinaison de ce dernier par rapport à l'horizontale.
L'énergie potentielle est nulle au sol (énergie de référence).
Les deux degrés de liberté donnent deux équations du mouvement issues du lagrangien
suivantes.
Les couples (énergies, variables généralisées) sont également formés.
Le mouvement du point matériel sur le plan est décrit par :
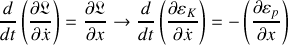
où effets d'inertie (issus de l'énergie cinétique) et force généralisée à l'origine du mouvement sont bien identifiés.
Ils donnent lieu à l'application directe du second principe de Newton selon la direction
:
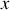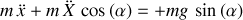
Les mouvements (accélérations) relatif (
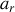) et d'entraînement (
) sont explicites.
Si le mouvement du point matériel est produit par la composante du poids
, apparaît en plus une force d'inertie (dû à l'accélération d'entraînement du plan)
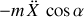et exprimant une liaison avec celui-ci, par le contact.
Le mouvement du plan incliné est décrit par le degré de liberté
:
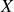L'absence de force généralisée d'origine conservative est à noter et une impulsion généralisée est conservée.
Les effets d'inertie et de contact permettent un mouvement selon :
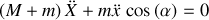
L'existence de l'accélération du plan est bien assujettie à celle du point matériel.
Cette équation permet de bien comprendre l'origine du recul du plan, et son accélération est :
.
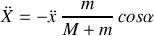Et l'inertie au mouvement du plan incliné est constituée par la masse totale du système.
Cette accélération permet de remplacer le terme d'entraînement subi par le point matériel et de déduire son accélération :
.
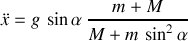Cette accélération exprimée dans le référentiel mobile est uniforme et ... supérieure à l'accélération du point matériel sur un plan incliné fixe, exprimée dans le référentiel fixe du plan. Ceci pour compenser le recul du plan incliné.
Ce phénomène est similaire à celui utilisé pour envoyer un satellite de plus en plus loin en le faisant rebondir sur des planètes massives.
Il s'agit alors d'une collision et le recul de ces dernières est utilisé par le satellite pour changer de direction mais également gagner de la vitesse.
Ces deux situations décrivent le résultat d'une conservation de quantité de mouvement entre deux corps en mouvement.
Remarque : Le cas particulier du plan fixe.
Le plan fixe est réalisé avec la condition :
Une inertie infinie du plan, soit
impliquant→
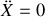et →
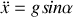
Une façon de vérifier les calculs ci-dessus.
Complément : Formulation vectorielle.
Dans une formulation newtonienne, les deux sous-systèmes (point matériel et plan incliné) sont séparés et décrits chacun par le second postulat de Newton.
Le point matériel a un mouvement plan, et deux composantes dans le repère fixe.
Le plan a un mouvement linéaire et une seule composante.
Si
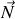est la force de contact avec le plan, les mouvements horizontaux et vertical de chaque partie sont obtenus via le système:
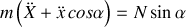
Sur le plan incliné isolé s'exerce l'action du point matériel
:
L'ensemble de ces équations décrit le même mouvement que celui des équations d'Euler-Lagrange précédentes.
Un petit plus néanmoins, la force de liaison peut ici être explicitée.
Complément :
Tous les calculs ci-dessus peuvent être évalués de manière approximative dans le cas d'un déséquilibre prononcé entre les masses (en faveur du plan incliné) pour avoir idée des ordres de grandeur des phénomènes observés.
Le chapitre VI traite des modifications à apporter au formalisme lagrangien lorsque le référentiel de description du point matériel est mobile.
Conclusion intermédiaire.
Dans les exemples présentés ci-dessus, les équations du mouvement ont été chaque fois décomposées autour de l'expression du lagrangien en énergies cinétique et potentielle.
Ces exemples ont permis de mettre en évidence les sources d'accélération généralisée (souvent en relation avec la variation d'énergie cinétique) et de forces généralisées (avec le travail des forces).
Cette séparation, des énergies et des rôles, simplifie grandement le schéma d'analyse.
Lorsque des contributions mélangées apparaissent, de l'entraînement et plusieurs référentiels peuvent être mis en jeu.
Dans l'exemple qui suit, une formulation séparant encore plus directement les énergies sera présentée avec le support lagrangien mais sans la fonctionnelle.
