Cet exemple traite d'un mouvement de translation (le long de la tige) s'ajoutant (et dû) à une rotation, contrôlée ou non, de la tige (Fig. 3) autour d'un axe vertical.
Le mouvement étudié est donc celui de la bille, un point matériel, affecté par le mouvement de la tige.
Il peut être traité d'une manière simple et directe si la rotation de la tige est connue.
Mais également susciter des pérégrinations entre différentes situations expérimentales.
Cette dernière démarche sera suivie car elle permet un questionnement sur les formalismes et leurs hypothèses.
A l'opposé de la règle habituelle, le cas général (complexe) sera le fil directeur.
Le cas particulier de la rotation uniforme de la tige, en apparence plus simple, apparaîtra au cours du développement.
Un cas intermédiaire est caractérisé par un lancer de la tige, avec une énergie cinétique initiale, produisant le déplacement de la bille.
Cette démarche est suscitée par une toujours possible erreur de mises en équations du problème. Elle donne un éclairage inattendu sur le cas simple mais également sur les différents formalismes.
Méthode : Autour du cas particulier d'une rotation uniforme
En toute généralité, deux variables spatiales peuvent intervenir dans la description puisque le mouvement s'effectue dans le plan horizontal Oxy.
La rotation de la tige autour de l'axe vertical
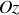induit un mouvement qui permet l'utilisation des coordonnées polaires
, dans la base orthonormée
qui tourne avec la tige.
Ceci permet également une démarche associée aux mouvements relatifs.
Dans le cas général, la tige tourne avec une vitesse angulaire notée
.
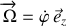Attention : Cas de la rotation uniforme
Si la rotation de la tige est entretenue et connue : par exemple
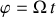, un seul degré de liberté permet de décrire le mouvement de la bille. Cette relation est une contrainte et réduit le nombre de degrés de liberté.
Concrètement, entretenir une rotation uniforme nécessite un moteur, une intervention extérieure sous forme de couple de rotation.
La question de la conservation de l'énergie totale peut alors se poser pour une rotation, uniforme ou non.
Méthode : Cas général
Cependant, la présence de deux coordonnées permet une analyse plus fouillée ainsi que la description de situations expérimentales les plus diverses.
Par exemple, un lancement initial de la rotation de la tige suivi d'un mouvement libre avec ou sans effet de frottement .
Plus formellement, les deux coordonnées permettent aussi de préciser la notion de degrés de liberté nécessaires (utiles) à la description.
Explication : Observations et méthode
Une réalité physique et générale apparaît : la bille s'éloigne du centre le long de la tige et un observateur tournant avec la tige, quelle que soit sa vitesse de rotation, constante ou non, ne verrait que ce mouvement d'éloignement.
Ce mouvement de la bille accéléré (mais pouvant être ralenti par quelque frottement) est décrit par la variable
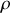(une distance positive), qui sera certes affectée par la rotation de la tige
.
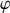Malgré leur couplage, le jeu de variables sera donc traité dans cet ordre de prédominance :
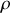puis
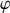en identifiant (pesant) le rôle de chacune.
Méthode : Éléments de lagrangien
La position de la bille dans le rail et dans le plan est repérée au moyen de :
.
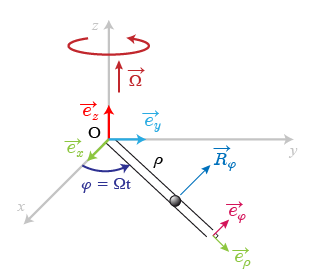
Le calcul de l'énergie cinétique de la bille nécessite la détermination de la vitesse.
Selon les notations adoptées, cette dernière s'écrit le plus généralement :
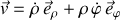
Et l'énergie cinétique :
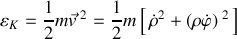
Elle est constituée par deux contributions additives : celles de la translation le long de la tige et de la rotation d'entraînement.
Aucun mouvement vertical n'est observé.
Nulle énergie potentielle de pesanteur n'intervient dans ce mouvement : l'effet de la pesanteur est compensé par celui de la réaction verticale du support.
Si les forces de frottement sont négligées et sans force additionnelle, le lagrangien se réduit à l'énergie cinétique.
Les équations d'Euler-Lagrange du mouvement conduisent à deux équations différentielles du second ordre qui seront analysées séparément.
Méthode : Équation pour la variable radiale.
La première équation, pour la variable
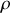, est :
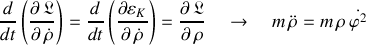
La variation temporelle de la quantité de mouvement le long de la tige trouve sa source directement dans la rotation de la tige, et l'existence de
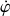, quelle qu'elle soit.
- Plus précisément, la pseudo force "centrifuge" est la source du mouvement radial.
En effet puisqu'aucun bord ne contient la bille, cette force d'inertie provenant de l'entraînement de la tige impose le mouvement de la bille.
Attention : Si la rotation est uniforme
Une solution analytique apparaît :
Pour le cas simple d'une rotation uniforme du rail (produite par un moteur), ce seul degré de liberté
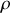conduit à une éjection «exponentielle» de la bille selon l'équation différentielle :
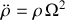.La solution générale s'exprime alors par
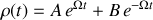.Les conditions initiales de la bille, en position et en vitesse, sont contenues dans les grandeurs
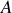et
.
Cette solution présente deux contributions : l'une sera dominante pour les temps très courts (l'exponentielle négative), la seconde prend le relais et est responsable de l'éjection explosive.
L'échelle de temps étant déterminée par
.
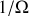Si la rotation n'est pas uniforme, la variable angulaire est régie par sa propre équation d'Euler Lagrange qui sera développée plus loin et qui couplera les deux variables.
Mais avant d'aborder ce cas et suite à cette analyse du mouvement le long de la tige, quelques observations additives peuvent être énoncées.
Elle permettent un retour vers la mécanique vectorielle, ouvrent des perspectives vers d'autres exemples et apportent des précisions sur la théorie lagrangienne.
Complément : Et les frottements
- La bille peut être soumise en plus à un frottement lors de son contact avec la tige ; celui-ci est radial mais peut dépendre de l'amplitude de la vitesse de rotation.
Il apparaîtra explicitement dans l'équation selon
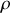, sous la forme d'une force de frottement visqueux
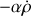par exemple.
Il s'opposera à l'éloignement et ralentira le jaillissement de la bille.
Mais en modifiant le mouvement radial décrit par
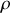, celui de la rotation de la tige le sera implicitement... via
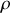, les équations étant couplées (voir ci-après).
Pour quantifier ce nouveau mouvement, la forme du lagrangien sera modifiée par la présence du frottement. (voir le chapitre 4).
- A l'opposé, un frottement sur le rail (au niveau de l'axe par exemple) affectera en priorité le mouvement de rotation, l'équation de
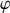, par le biais d'un moment résistif et dissipatif.
Puis par ricochet il affectera celui de la bille le long de la tige.
Dans ces cas, la vitesse angulaire ne peut être constante et deux degrés de liberté sont nécessaires pour décrire le mouvement de la bille.
Remarque : À noter
Quelques remarques générales :
La variable
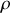est une grandeur positive.
L'accélération radiale apparaît toujours positive, impliquant un mouvement accéléré le long de la tige.
La vitesse radiale est ici positive.
Un frottement proportionnel à la vitesse peut, au plus, bloquer (stopper) la bille.
À présent l'évolution de la seconde variable
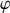peut être scrutée.
Méthode : Équation pour la variable angulaire
En l'état des hypothèses suivantes :
- frottements négligés, et
- origine floue de la rotation de la tige,
l'équation, régissant la variable angulaire (et la rotation de la tige), issue de la fonction de Lagrange ci-dessus, s'écrit :
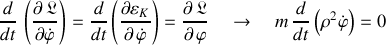
Cette équation pour la variable angulaire exprime la conservation au cours du temps d'une grandeur :
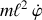qui est le moment cinétique de la bille.
Elle nécessite différents niveaux d'analyse.
Sept étapes de questionnement sont présentées dans le cheminement à deux variables.
Attention : 1. La "non problématique" de la rotation uniforme
L'équation pour la variable angulaire paraît incompatible avec celle décrivant la variable
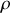dans le cas d'une rotation uniforme.
En effet, reporter la solution de l'éjection exponentielle dans l'équation d'évolution de la phase produit la réponse suivante :
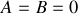. Mais la réalité de la tige qui tourne et de l'éjection de la bille est bien là.
Ce conflit apparent indique d'abord une application erronée du formalisme, à une variable généralisée qui n'en est pas une.
Pour la rotation uniforme de la tige, la justification pragmatique, et lagrangienne, est la suivante :
La variable
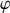n'est pas une inconnue (
).
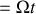→ Nul besoin de la garder comme variable à déterminer.
→ Ne subsiste donc qu'un seul degré de liberté.
Une réponse satisfaisante pour ce cas particulier.
Mais un message sous-jacent apparaît : le moment cinétique n'est pas conservé si la rotation de la tige est uniforme !
Plus d'informations seront accessibles en scrutant le problème sous d'autres angles.
Explication : 2. Communiquer avec une équation.
L'équation décrivant la rotation peut être déroulée autrement :
Avant de continuer l'investigation, une précision est utile :
Une vitesse angulaire positive implique une rotation dans le sens trigonométrique : le signe de la vitesse angulaire indique le sens de la rotation.
Un changement de signe de la vitesse de rotation
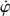indique seulement un changement du sens de la rotation.
L'équation admet deux solutions mathématiques qui sont :
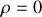, déjà obtenue et sans intérêt,
.
Cette seconde équation correspond à l'annulation de l'accélération
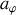de la bille selon la direction
.
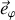Elle implique aussi l'équilibre entre deux termes :
l'un mettant en jeu, l'accélération angulaire et
l'autre, le produit des vitesses radiale et angulaire.
Dans le cas général, cette équation d'Euler Lagrange pour la variable
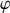exprime donc une accélération angulaire négative.
Ceci implique un ralentissement (freinage naturel) de la rotation, signe d'un mouvement non entretenu pouvant correspondre à un lancer initial de la tige.
Ce cas sera développé et intégré plus loin, avec un autre éclairage.
D'autre part, les deux termes peuvent être nuls simultanément :
Annuler l'accélération angulaire permet certes de retrouver une rotation uniforme mais elle revient à annuler l'accélération d'inertie
ou accélération de Coriolis et par conséquent, figer soit la rotation de la tige, soit le mouvement de la bille.
Ceci ne correspond pas à la réalité physique de l'éjection de la bille.
Et encore moins de la rotation uniforme.
Le moment cinétique n'étant pas conservé, que se passe t il donc dans le cas de la rotation uniforme ?
Explication : 3. Un peu d'intuition et d'expérimentation.
Sans rotation de la tige, la bille resterait immobile. Effet d'inertie oblige.
La situation particulière de la rotation uniforme est caractérisée par le fait que :
la rotation est entretenue par un couple moteur s'appliquant sur la tige.
→ la bille doit en ressentir l'effet : un effet subi.
Il faut imaginer le moteur d'une voiture : il produit une force motrice provenant de la pression des roues sur la chaussée, vers l'arrière. Le principe de l'action et de la réaction permet l'émergence de la force motrice, propulsant la voiture vers l'avant.
Plus prosaïquement, cette image est identique à celle qui permet la marche : appuyer sur le sol vers l'arrière... permet d'avancer.
Dans le cas de la bille, le mouvement de rotation, selon
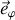, ne peut avoir lieu sans poussée dans cette direction.
Une poussée subie par un contact subi.
Qui dit poussée dit force de réaction.
Une approche en terme de forces permet également de visualiser l'effet de l'accélération d'inertie (
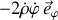) : il est de plaquer la bille sur le bord arrière de la tige, par rapport au sens de la rotation.
L'accélération étant portée par
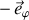), la force qu'elle produit l'est également.
Le contact qui s'en suit implique une réaction du support, en vertu du principe d'action et de réaction.
Une force de contact, notée
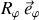apparaît en réaction à l'entraînement entretenu de la tige.
L'effet de cette réaction est de contrer celui de la force d'inertie de Coriolis et d'expliquer l'entraînement de la bille avec la tige.
Ce contact, résultant du mouvement du mouvement de la tige, n'apparaît pas naturellement dans le formalisme lagrangien.
En effet la notion de degré de liberté, correctement appliquée, permet d'éviter toute liaison et force de contact.
Dans le cas contraire, l'incompatibilité émergeant du cas particulier (rotation uniforme) est le signe d'un énoncé mal retranscrit et de non respect des hypothèses (règles) du formalisme : utiliser
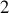variables dans un cas n'en comportant qu'une implique nécessairement une donnée supplémentaire, une contrainte. Et une modification du formalisme.
(voir Chapitre VI sur les multiplicateurs de Lagrange)
Explication : 4. Une rotation ? Le zoom du moment cinétique
L'équation d'Euler Lagrange régissant la variable angulaire
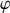implique la conservation au cours du temps d'une grandeur, le module du moment cinétique de la bille :
.
La direction de ce vecteur est celle de l'axe de rotation : la verticale.
Le moment cinétique de la bille est conservée si aucune source à sa variation n'existe. Alors l'accélération angulaire est négative : ceci décrit un mouvement de rotation freiné.
Lorsque le mouvement de la tige est entretenu, la bille subit la poussée de la tige et le moment de cette poussée contribue à la variation du moment cinétique : il n'est donc pas conservé.
La source de la variation est alors le moment de la réaction
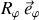, en écho au couple moteur qui s'applique sur la tige. Cette opération permet de transférer un couple moteur sur la bille, considérée séparément, et sans lequel la rotation uniforme de la bille ne peut être justifiée.
Complément : 5. Théorème du moment cinétique et formalisme lagrangien.
Dans le formalisme lagrangien et en cas de rotation uniforme, le degré de liberté associé à la rotation disparaît.
Mais le théorème du moment cinétique, lui, s'applique toujours à la bille.
Et son moment cinétique n'est pas conservé puisque la rotation est forcée (couple extérieur).
Ainsi la force de contact
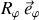possède un moment qui vaut :
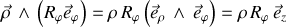
Ce moment de la force de contact a la direction du moment cinétique de la rotation .
Sa présence permet d'expliquer, en cas de rotation uniforme imposée, la variation au cours du temps du moment cinétique de la bille.
Le théorème du moment cinétique vient ainsi compléter le formalisme vectoriel du second principe de Newton.
Il génère un résultat additif : déduire l'allure de la force de liaison qui apparaît dans le PFD en même temps que celle d'inertie de Coriolis.
Le formalisme lagrangien, lui, ignore toutes ces forces et moments.
En effet, ce formalisme ne tient compte que des forces qui travaillent :
Ainsi il ignore cette force de contact dont il n'a aucun besoin pour suivre l'évolution de la bille le long de la tige.
De même, la force d'inertie de Coriolis n'apparaît pas en tant que telle dans le lagrangien en référentiel non galiléen. (voir chapitre 7)
Cette force est, de par sa définition, perpendiculaire à la vitesse.
Elle ne travaille donc pas et disparaît d'un formalisme énergétique.
L'incompatibilité avec la rotation uniforme de la conservation du moment cinétique est toujours générée par l'erreur sur les degrés de liberté.
Complément : 6. Forces, travail, énergies et... rotation libre
Cette description du système, non soumis à des frottements, permet de reconnaître une décomposition du PFD selon les directions
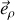et
.
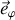En effet, l'écriture de l'accélération en coordonnées polaires :
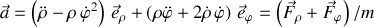
montre, qu'en l'absence de frottement sur la bille et selon
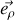, l'équation exprime une accélération radiale nulle.
L'équation d'Euler Lagrange pour cette variable est identique à ci-dessus.
Selon la direction orthoradiale, l'existence de
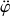est mise en œuvre d'abord par l'accélération de Coriolis
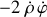, puis par toute force extérieure orthoradiale (frottements sur la tige par exemple).
Si un couple extérieur est présent, forçant ainsi l'allure de la rotation, alors le contact sur le rail doit être pris en compte et en réaction, la force de liaison
.
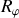Le travail de cette force de contact est nul selon
.
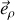Selon
, la puissance nécessaire au déplacement (fournie par le moteur par exemple) vaut
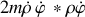en l'absence de frottements.
Exemple : 7. Rotation libre de la tige.
Le cas de la rotation libre autour de l'axe vertical, produite par une impulsion initiale, caractérise un système conservatif et une énergie cinétique initiale constante :
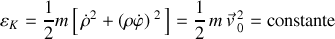
La somme des deux contributions est constante.
Si l'énergie de translation croît au cours du temps, utilisée par la bille pour s'éloigner du centre, l'énergie de rotation doit décroître.
Une énergie que la tige perd.
Le ralentissement de la rotation est ainsi prévisible.
Mais selon quelle équation et forme analytique ?
L'énergie mécanique totale se limitant à l'énergie cinétique, sa variation ou conservation au cours du temps est tributaire de l'expression générale suivante obtenue également par dérivation du carré de la vitesse :
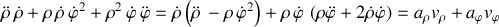
Elle correspond au produit scalaire entre les vitesse et accélération, et met en évidence la contribution "énergétique" de chaque terme.
Au vu de ce qui précède, l'équation selon la direction radiale est nulle : le signe de cette variation dépend donc complétement du second terme.
Ainsi la conservation de l'énergie mécanique totale implique nécessairement
soit
pouvant être reportée dans l'équation
pour obtenir une équation différentielle vérifiée par
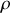
couplée à celle de
.
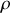Ces deux équations décrivent le régime transitoire vers un arrêt de la tige.
Ce régime permanent peut avoir lieu si la tige est suffisamment longue, la bille continuant son mouvement avec sa vitesse au moment de l'arrêt de la tige.
Toujours en l'absence de frottements.
Lorsque les deux degrés de liberté sont nécessaires, les équations sont couplées.
Preuve : Un calcul, une solution.
Le couple d'équations décrivant le mouvement sont :
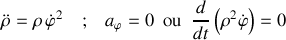
La dernière équation permet de trouver une première constante du mouvement, qui peut être corrélée à l'énergie initiale (
) communiquée à la tige et à la bille située en
:
Ceci permet de séparer les variables en remplaçant la vitesse angulaire dans l'équation pour
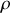pour obtenir l'équation différentielle décrivant la position de la bille :
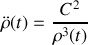
En multipliant par
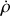, et effectuant une intégration, entre d'une part un instant initial où la bille se trouve sans vitesse en
et d'autre part un instant quelconque, la vitesse obtenue est :
.
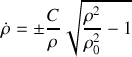Cette dernière équation est directement accessible par la conservation de l'énergie totale.
Avec un simple changement de variable et une séparation des variations, la solution apparaît :
.
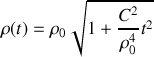Cette solution exprime une éjection de la bille moins explosive (brutale) qu'une exponentielle, plus contrôlée puisqu'elle participe à un échange d'énergie avec le mouvement de la tige.
Le ralentissement de la tige est régi par :
.
Sans frottements, l'arrêt de la tige s'effectue en un temps infini...
Attention : Degrés de liberté et variables généralisées
Ainsi après ces deux exemples, le rôle des coordonnées généralisées, en mécanique et probablement ailleurs, est à associer en termes de lois au sens de chacune.
Une variable exprimant une distance vérifie directement la seconde loi de Newton (PFD).
Alors qu'une variable angulaire décrit une rotation et vérifie le théorème du moment cinétique.
Chaque variable inconnue supplémentaire représente un degré de liberté additif.
En conclusion, la notion de degré de liberté, et de variable généralisée associée, implique la notion d'inconnue réelle.
C'est-à-dire une variable
non constante (évoluant au cours du temps) et
indépendante des autres.
Si ce dernier cas n'est pas réalisé, la relation liant les variables est appelée contrainte.
Le formalisme lagrangien permettra soit de réduire la dimension du problème soit d'utiliser une extension du formalisme basée sur la notion de multiplicateurs de Lagrange.
Complément : Perspectives
L'expression du formalisme en termes d'accélérations et de forces généralisées autorise des contributions additives aux équations d'Euler Lagrange.
Les forces de frottement par exemple, si elles sont connues, peuvent être ajoutées sous forme de forces de frottement généralisées et selon des règles qui seront précisées.
Intuitivement, un couple résistif peut expliciter un frottement moyen sur la surface de contact tige-sol ou au niveau de l'articulation entre la tige et l'axe de rotation, affectant ainsi directement la variable angulaire.
Si la notion de variables inconnues et de degrés de liberté pose problème, et si néanmoins des contraintes sont apparentes, les équations du mouvement d'Euler Lagrange mettant en jeu ces contraintes peuvent être également élaborées.
Le formalisme des multiplicateurs de Lagrange permet de conserver les degrés de liberté supplémentaires mais pour être associé ultérieurement et additivement à la forme explicite de la contrainte.
