Cet exemple est typique d'un système continu, de solide déformable.
Néanmoins le formalisme énergétique de Lagrange permet d'obtenir l'équation du mouvement sans difficulté.
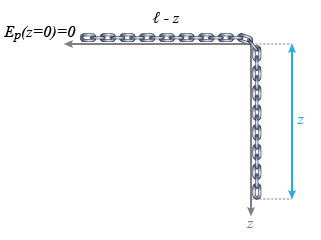
La chaîne (Fig. 6), ou la corde, est inextensible. Elle a une masse linéique (masse par unité de longueur) constante (cas homogène). Soit :
.
Le mouvement de glissement de la chaîne est provoqué par le poids variable de sa partie verticale, de masse
.
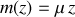Le seul degré de liberté du mouvement est ainsi la longueur de chaîne qui pend :
.
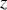Toute la chaîne se meut avec la même vitesse
.
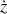L'énergie cinétique de la chaîne est donc :
.
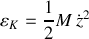Pour un déplacement
, la portion de chaîne à l'origine du mouvement produit un travail
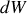et une variation d'énergie potentielle selon :
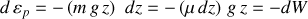
La relation entre accélération généralisée
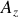et force généralisée
est alors :
De plus, pour un seul degré de liberté, les dérivées partielles se transforment en dérivée droite.
L'équation du mouvement s'écrit :
.
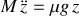La solution en est une forme exponentielle se déclinant selon le cosinus hyperbolique suivant :
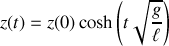
Le mouvement n'a lieu que si une longueur suffisante de corde pend, longueur à même d'assurer le démarrage du mouvement.
La validité de cette équation se limite à l'instant
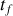pour lequel
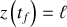.Une chute libre s'amorce alors pour le centre de gravité, avec des conditions initiales dépendant de cet instant limite.
La forme de la corde, ou chaîne, est quant à elle soumise à toute perturbation extérieure et dépend de sa rigidité (ou souplesse). Un paramètre ignoré jusqu'ici.
Complément : Extension possible de l'exemple.
Un exemple similaire conduisant au même type de mouvement "incontrôlable" (un emballement exponentiel) est celui de la machine d'Atwood.
Il décrit le mouvement libre de 2 masses reliées par une corde de masse non négligeable (une source d'énergie potentielle interne au système se transformant en énergie cinétique) passant sur la gorge d'une poulie, fixe ou en rotation.
La masse la plus lourde (et celle de la corde du même coté) agissant dans le sens du mouvement, l'autre masse (et la corde...) s'y opposant.
Si de plus la poulie tourne, une inertie additive apparaît via son moment d'inertie.
Rappel : Un classique... le problème à deux corps
Le dernier exemple qui sera développé permet de présenter un autre aspect du formalisme lagrangien.
Cette exemple a été traité dans le grain précédent, dans la partie 'la mécanique en termes d'énergies', pour explorer les limites de la conservation de l'énergie mécanique dans la description d'un mouvement dans un champ de Kepler.
