La démonstration qui suit est simpliste mais suffisante : une fonctionnelle
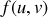de deux variables est utilisée pour passer vers une nouvelle fonctionnelle
.
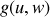Le transfert peut être effectuée parce que la nouvelle variable n'est pas quelconque.
Démonstration :
Les variables indépendantes
et
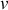sont reliées dans une fonction ‘potentiel’
.
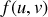La dérivée partielle
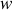est définie par :
Elle relie la nouvelle à l'ancienne variable.
La transformation de Legendre qui permet de passer de la fonctionnelle
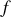à une nouvelle fonctionnelle
s'écrit :
où le rôle de
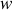est donc de remplacer
.
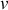Les relations suivantes permettent d'effectuer le passage d'un système à l'autre :
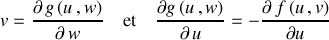
L'information portée par
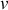est ainsi transférée vers
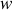, finalité de la transformation de Legendre
Cette transformation peut être directement appliquée au lagrangien.
Méthode : Du lagrangien au hamiltonien
Le lien entre ce qui précède et la mécanique lagrangienne apparaît via la fonction de Lagrange ou encore la correspondance :
les vitesses généralisées
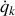devant être remplacées.
La nouvelle variable est l'impulsion généralisée :
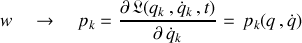
Cette relation permet de déduire
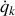en fonction de
.
Poursuivant la transformation, la nouvelle fonctionnelle s'écrit alors :
où la fonctionnelle
dépend à présent des coordonnées et moments conjugués généralisées, seules, puisque les vitesses généralisées disparaissent, remplacées par les moments conjugués.
Les équations complémentaires, dont celles du mouvement, peuvent être déduites de la transformation de Legendre selon :
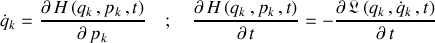
et :
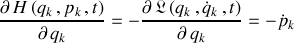
Les équations relatives à
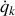et
donnent les équations d'évolution des deux familles de variables : elles correspondent aux équations du mouvement.
La dernière équation relie les dépendances temporelles explicites des deux fonctionnelles.
De fait, les équations relatives à
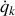sont celle du passage des anciennes vitesses aux moments conjugués.
