Cette série de
exemples sont des applications directes et comparatives de la transformation de Legendre.
Leur simplicité permet la mise en place de réflexes associés à son utilisation et l'analyse des apports de la transformation.
L'oscillateur harmonique
L'exemple classique le plus simple concerne le système à une dimension (
).
La démarche du lagrangien de ce système vers son hamiltonien commence par l'identification des variables généralisées et l'écriture des deux fonctionnelles.
Si
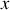et
sont les coordonnée et vitesse généralisées,
le lagrangien de l'oscillateur harmonique de constante de raideur
s'écrit : 
l'impulsion généralisée s'écrit :
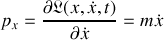, d'où est déduite la relation
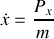
La forme générale et non finale de l'hamiltonien peut être déduite de la forme générale suivante :
La fonctionnelle de Hamilton de ce système conservatif s'écrit alors :
Les deux équations complémentaires sont alors :
qui renvoie la définition du moment conjugué généralisé et
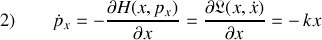
explicite l'équation du mouvement, une application directe du second principe de Newton, la force de rappel apparaît dans le second membre.
Et finalement,
,
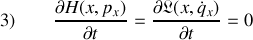une équation qui participe à la vérification de la propriété de conservation de l'énergie mécanique : le temps n'est pas explicite dans les
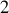fonctionnelles.
Rappel :
Le système conservatif produit un hamiltonien
indépendant du temps, tout comme le lagrangien.
Particule dans un champ de force cartésien
Cet exemple permet de traiter le plus général des problèmes conservatifs à
dimensions, l'énergie potentielle dépendant simplement des
coordonnées cartésiennes selon
.
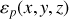La fonction de Lagrange dans ce cas est
Elle permet de déduire trois variables 'impulsions généralisées' selon la notation vectorielle (triplet) :
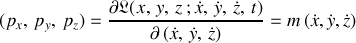
les
dérivées partielles sont relatives à chacune des coordonnées.
De cette dernière équation vectorielle, peut être déduite la forme vectorielle d'une des équations complémentaires :
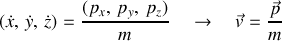
La fonction de Hamiltonien est alors obtenue selon :
Soit :
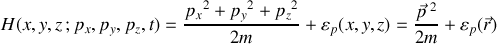
Il présente la propriété caractéristique d'un système conservatif : le système est soumis uniquement à une force dérivant d'une énergie potentielle.
Les équations du mouvement sont déduites de :
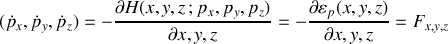
L'expression des composantes cartésiennes des forces est explicitée.
Selon les cas d'énergie potentielle étudiés, les équations du mouvement de Newton (vectorielles) sont obtenues.
Particule dans un champ de force central
Cette situation décrit également un mouvement à
degrés de liberté.
Du fait de l'interaction centrale en
,
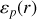étant la distance au centre de l'interaction, l'usage des coordonnées sphériques est adapté.
Le lagrangien s'écrit :
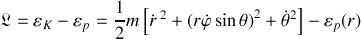
et donne lieu aux impulsions généralisées suivantes, sous forme vectorielle :
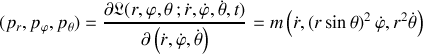
où les dérivées partielles sont respectives aux vitesses généralisées (linéaire ou angulaire).
Les impulsions associées aux variables angulaires sont les moments d'inertie relatifs aux axes de rotation (respectivement
, fixe et
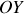mobile dans ce cas : cf référentiels non galiléens. Quantité de mouvement. problème à deux corps).
Le hamiltonien se présente alors sous la forme :
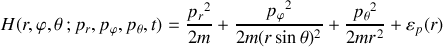
Les équations du mouvement sont intéressantes pour les 'impulsions associées aux phases',
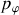et
puisque les équations du mouvement sont :
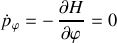
La constante du mouvement
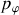apparaît rapidement.
L'évolution du moment angulaire
vérifie :
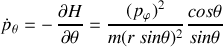
La discussion portant sur la conservation de
porte uniquement sur l'annulation du numérateur, soit
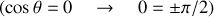comme précédemment.
L'élaboration de la fonctionnelle de l'hamiltonien étant effectuée, il est utile à présent retrouver une autre formulation des équations du mouvement du système mécanique.
Pour cela, un nouvel outil mathématique est préalablement utile : il s'agit des crochets de Poisson.
Une fois cet outil mis en place, les équations du mouvement seront à nouveau reformulées, toujours à la recherche de formes simples, symétriques et invariantes.
