Les variables "coordonnées" qui décrivent un système sont choisies selon des critères précis.
Elles sont linéairement indépendantes.
Sinon les contraintes (et équations) qui les lient sont
soit utilisées pour réduire le nombre de degrés de liberté et aller vers de nouvelles coordonnées généralisées,
soit introduites dans la description à un moment judicieusement choisi de la résolution du problème ou via des multiplicateurs de Lagrange.
Les variables "vitesses" ou "impulsions" suivent les règles imposées par les formalismes, lagrangien et hamiltonien.
Ces
variables, soit le double du nombre de degrés de liberté, sont indépendantes.
Lorsque les couples de variables (
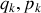) sont déterminés et choisis, toutes les fonctionnelles du formalisme hamiltonien vont s'exprimer en fonction de ces variables.
Les crochets de Poisson peuvent également être appliquées à ces variables.
Elles sont alors reliées entre elles selon les définitions suivantes.
Définition :
Les variables (
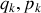) sont canoniquement conjuguées car elles vérifient les crochets de Poisson suivants :
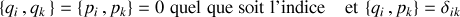
Ces propriétés sont directement issues de l'indépendance des variables entre elles.
La fonctionnelle "hamiltonien" dépendant de ces variables canoniquement conjuguées, le formalisme hamiltonien est canonique.
Explication : Variables canoniquement conjuguées - variables indépendantes.
Les crochets de Poisson des variables du problème expriment l'indépendance les unes par rapport aux autres des
variables (coordonnées et moments conjugués) du système mécanique.
En effet, si les dérivées partielles sont notées
et
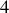dans l'ordre de la définition des crochets de Poisson,
le premier crochet de Poisson s'annule parce que
et
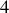sont nulles,le second s'annule parce que
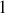et
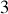sont nulles,et dans le dernier, le symbole de Kronecker exprime que seules les dérivées partielles des variables par elles-mêmes sont non nulles.
De plus, l'ordre entre coordonnées et impulsions généralisées permet d'écrire ces troisièmes crochets sous la forme :
.
Ceci est vrai pour les crochets de toute fonctionnelle.
Complément : Variables canoniquement conjuguées et temps en mécanique classique.
L'importance de cette propriété entre ces couples particuliers de variables (la coordonnée et son conjugué) prend un sens spécial via les relations d'Heisenberg.
Ces dernières associent leurs variations sous forme d'un produit fini (de l'ordre de
), ce qui, en mécanique quantique et pour les systèmes de faibles dimensions, permet de traduire l'influence de la méthode (ou de l'appareil) de mesure sur la mesure elle-même : la précision de mesure sur une variable augmente l'imprécision sur l'autre.
Les théories probabilistes et la mécanique quantique en découlent.
Un second couple de variables est également mis en jeu dans les relations d'Heisenberg, il s'agit du temps et de l'énergie... à l'origine de la théorie de la relativité.
Le temps est uniforme dans les formalismes classiques et il n'apparaît pas comme une "variable" comme les autres.
Néanmoins son rôle redevient notable lorsque l'énergie totale se détériore.
Les énergies, quant à elles, sont multiformes et combinées dans des fonctionnelles aux propriétés particulières, à l'image des transferts qu'elles produisent.
Le couple (temps, énergie) a donc nécessité une révolution scientifique pour sa mise en place.
Attention : Les variables canoniques sont elles uniques ?
D'autres variables canoniques généralisées peuvent être obtenues si elles vérifient les conditions ci-dessus.
Les transformations qui les produisent sont dites canoniques.
En complément, partant d'un ensemble de variables estampillées canoniques et toujours à la recherche de la description la plus simple d'un système, des fonctionnelles aux propriétés particulières peuvent être obtenues si des transformations sont réalisées via des "changements de variables canoniques".
Les exemples ci-après permettent de saisir les grandes lignes de passage d'un système de variables à l'autre via des transformations, avant de définir quelques transformations canoniques.
Explication : Exemple et contre exemple de variables canoniquement conjuguées.
Les exemples couramment utilisés, car plus expressifs, sont ceux relatifs à l'oscillateur harmonique
et dont l'hamiltonien est exprimé comme suit :
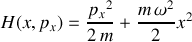
La constante de raideur
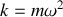est remplacée par son expression en fonction de la pulsation propre
.
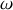La transformation suivante assure le passage de
vers
:
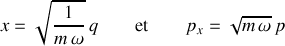
Elle présente une symétrie de forme.
Son inversion conduit à la symétrique alternée entre les variables :
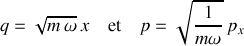
Le calcul des crochets de Poisson des nouvelles variables donne :
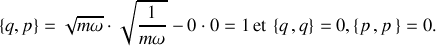
ce qui constitue une signature de nouvelles variables canoniquement conjuguées et de transformation canonique.
Un nouvel Hamiltonien peut être dérivé :
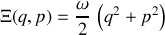
lequel présente une forme simplifiée (représentation circulaire dans l'espace des phases).
De plus, il génère les mêmes équations du mouvement que pour le jeu de coordonnées
:
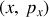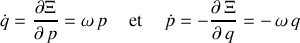
Ainsi la transformation effectuée est canonique et elle laisse invariante les équations du mouvement.
Fondamental :
Une transformation canonique permet le passage d'un espace à un autre de variables canoniquement conjuguées.
De plus, elle laisse les équations du mouvement invariantes.
Exemple : Oscillateur harmonique complexe.
La transformation ci-dessus est légèrement modifiée pour obtenir le hamiltonien suivant :
Partant de là, un second changement de variables est effectué :
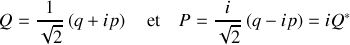
Il mélange coordonnées et impulsions et joue subtilement avec les phases pour créer deux nouvelles variables indépendantes.
Cette transformation canonique, et complexe, s'avère fort utile en mécanique quantique.
Elle est canonique puisque :
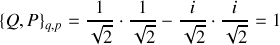
Le nouvel hamiltonien obtenu
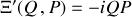est original (complexe) et loin de la forme quadratique propre à l'oscillateur harmonique.
De plus, les équations du mouvement,
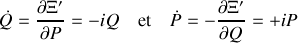
sont également complexes et... découplées.
Les constantes d'intégration doivent être complexes pour rester en accord avec les équations du mouvement et assurer la dimension "phase" introduite par la transformation canonique.
Le retour aux variables initiales, réelles, redonne la solution oscillante prévue, notamment :
où
et la phase de la variable
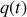est uniquement contenue dans
.
Remarque : Et les lagrangiens ?
La symétrie qui apparaissait dans la transformation de
vers
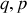et qui devenait explicite et visuelle dans le calcul des crochets de Poisson transforme également le lagrangien de l'OH de :
Les deux lagrangiens décrivent bien le même système.
Les constantes multiplicatives ne jouent aucun rôle ; elles ne modifient pas la solution.
Un changement d'échelle de temps du type
permet une écriture du lagrangien (et du hamiltonien) encore plus réduite.
Attention : Contre-exemple.
À titre de contre-exemple, la transformation suivante n'est pas canonique :
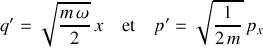
Elle est déséquilibrée entre ses paramètres, notamment.
Alors que son hamiltonien est donné par
, les équations du mouvement sont respectivement :
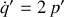et
.
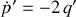Les nouvelles variables ne peuvent décrire le même système que le couple précédent, réduisant le domaine de validité à la valeur
.
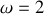En effet l'évaluation des crochets de Poisson
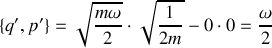
ne vaut l'unité que pour cette valeur particulière de
.
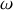