Le formalisme de Hamilton s'appuie sur les deux ensembles de variables,
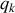et
.
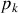Leur ordre est important dans la définition suivante :
Définition :
Si
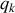et
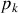sont des variables canoniquement conjuguées, les crochets de Poisson de deux fonctionnelles
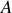et
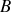, fonctions de ces couples de variables, est défini par la relation :
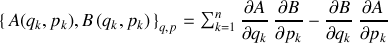
L'ordre des variables est précisé en indice aux crochets.
Remarque :
Le temps ne joue aucun rôle dans cette formulation de mécanique classique.
Ceci met encore en évidence son rôle très particulier : ce n'est pas une "variable" au sens de "grandeur choisie pour décrire le système".
Le temps est là ; il s'écoule. Et les variables en dépendent.
On peut le figer pour un calcul précis, comme une photographie, un instantané.
Dans la définition des crochets de Poisson, apparaît la notion de conjugaison canonique laquelle exprime des variables et moments de variables indépendants comme le confirme la définition à venir dans le paragraphe suivant.
Propriété : Propriétés des crochets de Poisson
Ces propriétés permettent de déduire des lois régissant le mouvement et caractérisant le système étudié.
1) La plus simple :
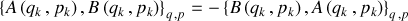
est une propriété due à l'ordre choisi pour le couple (coordonnée - impulsion).
2) La distributivité par rapport à l'addition :
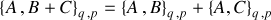
est déduite de celle de la dérivée partielle.
3) La distributivité par rapport à la multiplication traduit la propriété de la dérivée d'un produit de fonction :
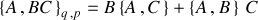
Et finalement 4) l'identité de Jacobi
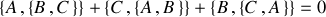
qui met en relation
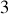fonctionnelles.
Ceci permet de propager des propriétés particulières susceptibles de décrire le système étudié.
Par exemple, si certains crochets de Poisson sont nuls, cela permet de déduire des relations entre fonctionnelles voire de trouver une nouvelle fonctionnelle, une nouvelle loi.
