Les variables, coordonnées et impulsions, étant définies ainsi que la fonction de Hamilton, il reste à déterminer les équations décrivant l'évolution du mouvement.
Pour cela, l'expression de la dérivée totale par rapport au temps de toute fonctionnelle
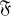s'écrit en fonction des crochets de Poisson.
Ainsi le plus généralement :
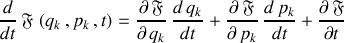
Les équations canoniques de Hamilton étant utilisées, la dérivée temporelle s'écrit :
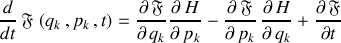
La forme élégante suivante est aisément déduite :
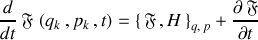
où l'ordre des crochets et des dérivées est indiqué.
Une propriété importante apparaît ainsi pour toute fonctionnelle
:
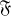Fondamental : Constante du mouvement
La fonctionnelle
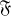est une constante du mouvement si
1) elle ne dépend pas explicitement du temps et
2) ses crochets avec l'hamiltonien sont nuls :
.
Toutes les constantes du mouvement sont ainsi aisées à déterminer.
De même, les crochets de Poisson permettent d'écrire les équations canoniques du mouvement de Hamilton sous une nouvelle forme.
Définition :
Les équations du mouvement de Hamilton formulées au moyen des crochets de Poisson sont :
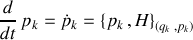
définissant ainsi les
équations différentielles du premier ordre, symétriques pour les variables canoniques
.
Complément : et remarque
Un parallèle peut être établi entre cette formulation simplifiée des équations du mouvement en mécanique classique et celle qui sera développée pour l'étude des systèmes atomiques et nucléaires en mécanique quantique.
Pour un système intégrable conservatif à
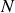degrés de liberté, il existe
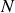variables d'action constantes du mouvement.
La propriété
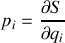(action =THJ) permet de définir une action réduite
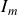sur un contour fermé
et telle que :
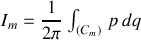
Ainsi la quantification EBK (Einstein, Brillouin, Keller) postule qu'à une constante près, seules les actions multiples entières du quantum (
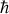) sont autorisées (lorsque ces actions sont constantes) selon :
où
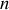est un entier et
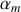est le coefficient de Marslow.
Et le formalisme classique de Hamilton rejoint celui quantique.
Exemple : Intégrale première
La première grandeur physique qui est conservée ... pour les systèmes conservatifs, est l'hamiltonien lui-même.
L'origine de cette intégrale première est l'hamiltonien qui est indépendant explicitement du temps : (
).
Ainsi le piégeage d'une charge électrique (
) par un conducteur est décrit par
où
.
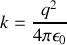Cet hamiltonien provient de la notion d'image électrostatique : la charge influence le conducteur, créant une charge interne au conducteur (-q), en position symétrique à la charge externe, et dans le champ de laquelle elle va se trouver piégée.
Près du conducteur, ce champ est perpendiculaire à sa surface : d'où une interaction selon la seule direction
.
Cette intégrale première est à l'origine de trajectoires dans l'espace des phases (
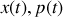) décrites par l'équation :
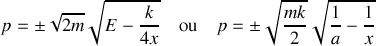
La seconde expression est dérivée pour une charge initialement au repos en
.
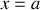La charge est attirée sur les impulsions négatives (elle est freinée) et revient au point initial avec des impulsions positives. Le changement de signe de l'impulsion s'effectue sur la paroi, comme tout rebond.
La période associée à ces trajectoires fermées est :
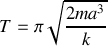
Ces trajectoires peuvent être simulées numériquement ; pour visualiser l'évolution au cours du temps de la particule sur sa trajectoire, il faut revenir à la vitesse
.
