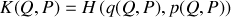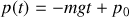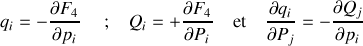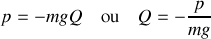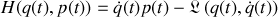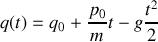Mouvement plan et champ central
Dans le cas d'une particule élémentaire, le théorème du moment angulaire (ou cinétique) appliqué au champ central indique qu'en cas de conservation de celui-ci, le mouvement est plan et s'effectue dans le plan perpendiculaire au moment angulaire.
L'inverse est -il vrai ?
Ou encore un mouvement plan est -il synonyme de moment angulaire conservé?
Pour répondre à ces questions, il faut mettre en équations l'hypothèse et poser les notations :
le mouvement se déploie dans le plan
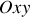; un choix possible est d'utiliser des coordonnées cartésiennes assurant ainsi un référentiel fixe. Et la particule de masse
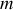se déplace avec une vitesse
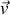telle que :
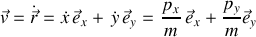
Son moment cinétique ou moment de la quantité de mouvement s'écrit alors :
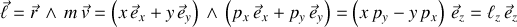
L'utilisation du formalisme canonique nécessite l'écriture du hamiltonien le plus général à deux dimensions :
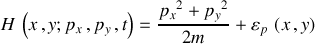
L'évolution au cours du temps du moment angulaire
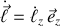indique que si sa direction est constante, son module ne l'est pas forcément.
Le calcul, avec les crochets de Poisson, de l'évolution au cours du temps du module du moment cinétique produit
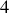termes selon :
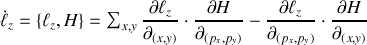
permet d'obtenir :
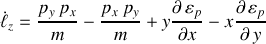
La conservation du moment angulaire produit la condition sur l'énergie potentielle suivante :
,
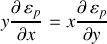entraînant la proportionnalité selon
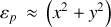ou une puissance de
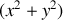, résultat obtenu par séparation des variables et intégrations partielles.
Le choix des plans
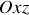ou
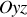aurait produit la même allure pour l'énergie potentielle.
En conclusion, le moment angulaire est conservé uniquement pour une énergie potentielle de type central et... une force centrale : une force dont le moment est nul.
Application au champ électromagnétique
Le moment, ou impulsion généralisée, apparaît souvent comme proportionnel à la vitesse, linéaire ou angulaire, le coefficient de proportionnalité étant la masse ou le moment d'inertie.
Les coordonnées cartésiennes en sont un exemple.
Mais lorsque l'interaction dépend de la vitesse, comme dans l'interaction de jauge, ce n'est plus le cas même en coordonnées cartésiennes.
Le lagrangien d'une particule chargée dans un champ électromagnétique, décrit par ses potentiels vecteur
et scalaire
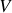, s'écrit :
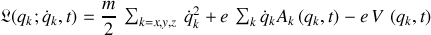
Les moments généralisés
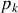s'écrivent :
Pour écrire l'hamiltonien du système, l'équation pour les moments est inversée pour donner
laquelle est reportée dans l'expression de l'hamiltonien :
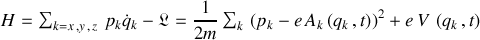
Les équations canoniques (notamment
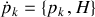) redonnent l'équation du mouvement de la particule chargée soumise à une force de Lorentz.
Chute libre et transformation canonique
L'objectif d'une transformation canonique est de permettre une étude du problème physique dans un espace de variables simplifié, réduit. Pour cela il faut transformer l'espace des variables en utilisant les lois de conservation et les variables cycliques.
L'exemple le plus simple qui soit est ici traité au moyen d'une fonction génératrice de type
: la chute libre à une dimension.
Le choix de la génératrice de type
a été orienté par le souci d'apporter un complément de cours au paragraphe sur les fonctions génératrices.
Cette exemple est traité sous forme d'exercice guidé et de jeu.
Méthode : Analyse dans le formalisme canonique
La démarche s'effectue autour de
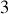questions principales :
Quelle grandeur est conservée ?
Anciennes, nouvelles coordonnées : quelle transformation canonique est possible ?
Comment utiliser la génératrice de type
pour effectuer la transformation ?
Pour effectuer une transformation vers une grandeur conservée, il faut identifier cette dernière !
1 ) Pour cela rien de tel que le cheminement rituel : du lagrangien
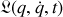, déduire le hamiltonien
et les grandeurs conservées.
Dans le cas de la chute libre 1-D, ni la coordonnée généralisée, l'altitude q(t), ni son impulsion conjuguée, la quantité de mouvement
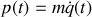, ne peuvent être des constantes du mouvement : sinon pas de mouvement.
Il reste à scruter du coté des fonctionnelles, lagrangien et hamiltonien. Aucune ne dépend explicitement du temps et notamment les crochets de Poisson de l'hamiltonien avec lui même est nul, signe que cette fonctionnelle est conservée.
Un premier résultat :
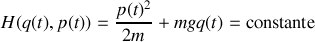
Le champ de pesanteur, cas particulier du champ gravitationnel, est conservatif : l'énergie mécanique totale de la particule en chute libre est conservé.
2 ) En cas de transformation canonique, de l'espace de variables (
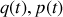) vers un espace de variables (
) où la grandeur conservée trouve sa place, la première question qui se pose est relative aux équations qui permettent le transfert de variables.
Question immédiate suivante : quid de la grandeur conservée ? Un choix qui peut être associée à la fonction génératrice, ici
. Cette génératrice conserve toutes les impulsions : ancienne et nouvelle.
Ainsi la nouvelle impulsion généralisée peut être proportionnelle à la grandeur conservée : c'est une énergie
où
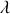est une constante.
Pour le choix de la nouvelle coordonnée généralisée, une aide est apportée par les crochets de Poisson des nouvelles variables :
Le choix le plus simple pour la nouvelle coordonnée est :
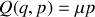de sorte que la transformation est canonique si la condition
est réalisée.
Avec la condition
les relations de transformation s'écrivent :
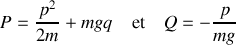
La transformation peut être inversée pour obtenir que le nouvel hamiltonien
... n'est rien d'autre que H !
La transformation canonique conservant les équations canoniques du mouvement, ces dernière permettent d'obtenir les équations différentielles du mouvement suivantes et leurs solutions :
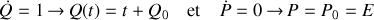
Ainsi les solutions
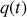et
sont intégrées, en fonction des conditions initiales.
La familiarisation avec la transformation a été effectuée. À présent, la partie "fonction génératrice" peut être abordée.
3 ) Les variables de la fonction génératrice sont telles que
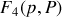et le nouvel hamiltonien est toujours :
La génératrice ne dépend pas explicitement du temps.
Pour trouver la fonction génératrice, il faut dériver, selon le modèle développé dans ce cours pour la fonction génératrice
, puis utiliser les équations générales de la transformation.
Ces équations, déduites du principe de moindre action, permettent de dériver à partir de la fonction génératrice les variables complémentaires (non retenues dans la fonction génératrice). Dans ce cas,
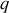et
.
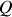Ainsi l'expression de
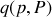permet de déduire par intégration la forme suivante pour la génératrice :
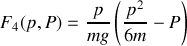
laquelle permet de retrouver
et de vérifier que la transformation est canonique et les variables sont canoniquement conjuguées (règles de "canonicité" qui remplacent celles des crochets de Poisson).
Comme précédemment, partant du hamiltonien
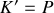et des équations canoniques du mouvement qui sont invariantes, les solutions
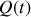et
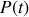sont obtenues ainsi que les expressions de
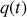et
.
Rappel : ou Schéma méthodologique des acquis
Les parties de cours à connaître ou visiter sont donc successivement.
Construction du lagrangien et ses propriétés
La transformation de Legendre, l'hamiltonien, coordonnées canoniques et les équations canoniques du mouvement.
La transformation canonique : anciennes et nouvelles variables.
Crochets de Poisson.
Les équations de passage (de transfert). Les équations inverses
Les fonctions génératrices et les équations générales de la transformation.
Application à la génératrice
.
Preuve : Preuves ou Équations en vrac
Et dans tous les sens.
Pour rétablir ces équations dans le sens des questions, sous entendues ci-dessus, il faut avoir compris le sens du chapitre.
