Dans ce chapitre, une reformulation de la mécanique classique issue du formalisme lagrangien est présentée.
L'un des intérêts de cette nouvelle formulation, outre de décrire une famille de problèmes, les systèmes hamiltoniens, est d'avoir facilité la construction théorique de la mécanique quantique et la mise en équation de "l'infiniment petit".
Sur le plan pratique, comment s'effectue ce passage de "Lagrange vers Hamilton" ?
Ce sera le premier point abordé. Il sera essentiellement orienté vers la syntaxe et les outils du formalisme.
Puis seront déployés les apports de ce formalisme à la modélisation des systèmes complexes, toujours vers une recherche de propriétés particulières susceptibles de réduire la complexité.
Ainsi ce formalisme canonique définit des variables canoniquement conjuguées (VCC) dont les caractéristiques d'indépendance en mécanique classique peuvent se transformer en propriétés particulières, en mécanique quantique par exemple.
De même les transformations canoniques permettent des changements de variables (VCC) et donc de passer d'un espace de phases (de description) à un autre espace, suivant des trajectoires particulières du problème étudié :
ces transformations laissent invariantes les équations du mouvement et
elles peuvent transférer la description vers des variables (CC) conservées.
Ce formalisme élabore donc de nouvelles règles de modélisation.
Les bases du formalisme lagrangien sont les suivantes.
L'action
vérifie le principe de Hamilton, soit :
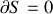, pour une trajectoire de l'espace des configurations (ou des phases). Ce principe variationnel utilise le lagrangien pour définir l'action et conduit au formalisme de Lagrange.
Il utilise
variables indépendantes (les coordonnées généralisées
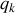et leurs vitesses associées
), issues de
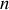degrés de liberté pour décrire le système mécanique. Ces variables décrivent l'évolution du système au moyen de
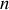équations différentielles du second ordre.Avec la comparaison des trajectoires possibles pour déterminer celle qui optimise l'action, le formalisme lagrangien relie, dans ces
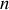équations, les
variables considérées comme à priori indépendantes.
Que deviennent ces bases dans le formalisme hamiltonien ?
Le formalisme canonique est construit sur un ensemble de
variables canoniquement conjuguées et une nouvelle fonctionnelle, l'hamiltonien, déjà élaborée dans le chapitre sur les lois de conservation.Ce formalisme permet de décrire l'évolution du système au moyen de
équations différentielles du premier ordre. Mais avant cela, il faudra remplacer une partie des variables, les
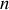vitesses généralisées du formalisme lagrangien, par
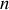nouvelles variables : les impulsions généralisées ou moments conjugués, définis par le formalisme lagrangien.La transformation qui permet le passage entre les deux formalismes s'inspire de la transformation de Legendre suivante.
Rappel : La transformation de Legendre
Cette transformation est bien connue en thermodynamique pour passer d'une fonction d'état à une autre, d'un potentiel thermodynamique à un autre selon le système étudié et partant de l'énergie interne
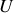.À partir
des
variables d'un problème thermodynamique : pression
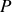, température
, volume
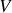et entropie
, et de
l'énergie interne
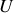dont la variation
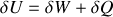est obtenue en sommant le travail effectué
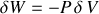et la quantité de chaleur produite, proportionnelle à la variation de température du système.
Trois fonctions d'état sont élaborées présentant chacune des caractéristiques particulières, selon les conditions expérimentales.
L'enthalpie définie par :
L'énergie libre par :
Et l'enthalpie libre :
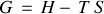
Ces transformations permettent de choisir les fonctionnelles intégrant simplement les propriétés expérimentales particulières aux divers processus thermodynamiques.
Ainsi le rôle particulier de la fonction enthalpie dans la description d'un processus isobare est bien connu.
Pour des transformations réversibles et selon que les expériences ont lieu
à volume constant où
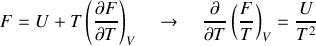
ou à pression constante où
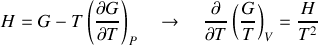
Ces relations utilisent les propriétés intrinsèques du système étudié pour déduire les lois les plus simples pour le décrire en mettant en jeu les fonctionnelles et les variables appropriées.
Cette méthode est utilisée pour passer de la fonctionnelle lagrangienne à celle hamiltonienne.
En mécanique, le formalisme lagrangien utilise déjà des relations adaptées ou contraintes pour réduire le nombre de degrés de liberté (variables réellement inconnues) et ainsi simplifier la description du système physique.
Il permet de s'affranchir de la notion de force la remplaçant par celle d'énergie.
Ces acquis du formalisme lagrangien sont transmis à l'hamiltonien.
Il reste que les équations du mouvement obtenues sont du second ordre.
Avec le formalisme hamiltonien, des simplifications additive sont attendues en termes de grandeurs conservées et d'invariants.
Et l'utilisation de
variables linéairement indépendantes pour
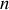degrés de liberté devraient permettre l'émergence de sous-espaces possédant des propriétés particulières propres au système étudié.
