Le paragraphe précédent a explicité les multiples possibilités pour décrire un système physique.
En effet, partant d'un jeu de variables canoniquement conjuguées, de nouveaux ensembles de variables peuvent être construit au moyen de transformations.
Certaines transformations possèdent des caractéristiques particulières selon la définition suivante.
Définition : La transformation canonique
Si un ensemble de variables
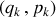est canoniquement conjuguées, la transformation qui permet le passage de
à
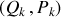est canonique si les nouvelles variables vérifient les crochets de Poisson suivants :
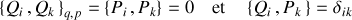
et donc sont également canoniquement conjuguées.
La transformation canonique permet le transfert entre deux ensembles de variables canoniquement conjuguées.
Fondamental :
Cette transformation garantit des équations canoniques du mouvement, invariantes de forme.
En effet, les nouvelles variables définissent un nouvel hamiltonien noté
et les équations canoniques du mouvement s'écrivent :
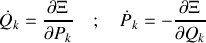
comme démontré dans les exemples précédents.
Cette propriété certifie un changement d'espace de description (variables) sans altération du mouvement.
La démonstration de cette invariance utilise la génératrice de la transformation canonique comme pour la fonction génératrice
ci-après : ainsi pour un système conservatif où les hamiltoniens, ancien et nouveau, sont égaux, et en utilisant les crochets de Poisson croisés des variables, l'invariance des équations canoniques lors du passage de l'espace (
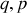) à (
) est nécessaire pour réaliser l'égalité des lagrangiens.
Pourquoi ces transformations ?
L'intérêt des nouvelles variables, du nouvel hamiltonien, est d'utiliser les outils les plus simples pour une description la plus simple.
Ainsi pour un problème à
degré de liberté (donc
inconnues réelles),
variables sont utilisées dans les formalismes lagrangien et hamiltonien.
Selon le problème étudié, certaines variables peuvent être conservées et entraînent des propriétés spécifiques.
Ceci peut réduire d'autant la complexité de la description.
Quelle est donc la description qui met en évidence le plus rapidement possible ces propriétés ?
Exemple : La méthode de Hamilton-Jacobi : une transformation particulière.
C'est la transformation canonique qui permet le passage vers un système de variables canoniques
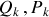constitué par
constantes du mouvement.
L'espace de configuration ainsi obtenu est stationnaire.
Dans ce cas, les équations du mouvement correspondent à :
et
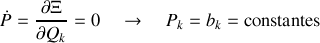
de sorte que l'inversion de la transformation permet de déduire les anciennes variables :
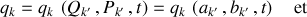
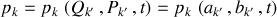
Pour construire cette transformation, une méthode progressive est nécessaire.
L'utilisation des fonctions génératrices suivantes en est une étape.
Pour la construction de ces fonctions génératrices, il n'est pas nécessaire que l'ensemble des
variables, de départ et d'arrivée
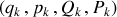, soit constitué de variables toutes indépendantes.
De fait, seuls
d'entre elles doivent l'être d'où le choix de garder une partie des anciennes variables
ou
.
Ainsi
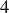possibilités, toutes équivalentes, s'offrent selon le choix de variables considérées comme indépendantes :
Si les couples
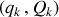sont choisies, la génératrice est conventionnellement notée
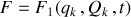
Si les couples
sont choisies, la génératrice est
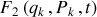
Si les couples
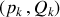sont choisies, la génératrice est
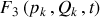
Si les couples
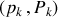sont choisies, la génératrice est
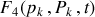
Méthode : Génératrice de type 2
La construction de la fonction génératrice s'appuie sur le principe variationnel et ses propriétés.
Dans le cas particulier d'une génératrice de type
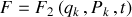, les variables restantes,
et
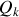, dépendent nécessairement des nouvelles variables
, choisies linéairement indépendantes, selon :
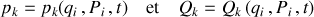
De sorte que l'inversion des
nouvelles impulsions :
en fonction des anciennes variables sont remplacées dans les
positions généralisées selon :
.
Ceci revient de fait à écrire
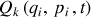et ainsi effectuer une inversion complète des nouvelles variables en fonction des anciennes.
Le principe variationnel s'écrit :
Le passage aux nouvelles variables produit un nouveau lagrangien tel que :
.
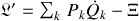Pour décrire la même physique en toute généralité, la relation entre les deux lagrangiens doit être générée par une fonction génératrice
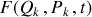(dans le cas général) selon :
Dans le cas de la fonction génératrice
, la dérivée temporelle totale s'écrit :
Cette dérivée temporelle peut être reportée dans l'égalité des lagrangiens, source d'une relation entre les hamiltoniens
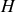et
.
Une identification entre les facteurs des variables indépendantes,
, seules susceptibles d'apparaître dans la formulation du principe variationnel (minimisation de l'action), permet de déduire les trois équations suivantes :
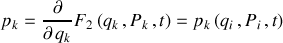
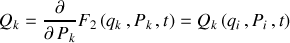
La première équation provient de l'annulation directe des termes
.
La seconde équation contient notamment un terme en
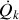, issu de
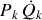, transféré vers
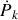, qui est la variable indépendante.
Ce transfert est effectué par une intégrale partielle sur le temps menée au cours du calcul de variation de l'action.
Cette opération permet de regrouper et d'annuler les termes en
.
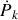La dernière équation contient les termes restants et devant s'annuler mutuellement : les hamiltoniens, nouveau et ancien, ainsi que la dérivée partielle temporelle de la génératrice.
Chaque fonctionnelle doit être exprimée dans sa représentation propre et ses variables.
Cette méthode permet alors soit
de dériver le nouvel hamiltonien connaissant la génératrice
soit d'accéder à la génératrice
à l'origine de la nouvelle description.
Exemple : Retour à la transformation de Hamilton-Jacobi
Dans le cas de la transformation de Hamilton-Jacobi, la dernière équation reliant les hamiltoniens, ancien et nouveau, utilise la relation radicale
pour assurer de nouvelles 'variables' généralisées... constantes.
Avec la notation suivante pour la génératrice :
,
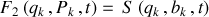les impulsions sont
.
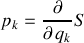L'équation de Hamilton -Jacobi est alors une équation différentielle pour la génératrice, déduite de l'équation :
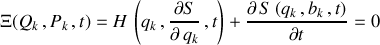
Cette équation permet de déduire la forme de la génératrice
.
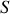La méthode générale donne
équations différentielles du premier ordre dont les constantes d'intégration sont les constantes
.
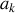Une fois la génératrice S connue, les équations s'écrivent :
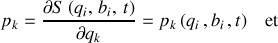
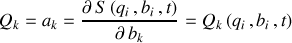
Ainsi toutes les grandeurs décrivant le système, avant et après la transformation, sont déterminées.
Fondamental : Transformation de Hamilton-Jacobi et principe de moindre action.
La fonctionnelle
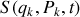, génératrice de la transformation de Hamilton-Jacobi, est telle :
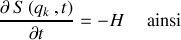
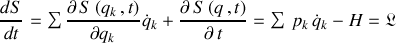
La génératrice de la transformation de Hamilton-Jacobi (THJ) n'est autre que la fonctionnelle "action" du principe de moindre action de Lagrange Hamilton.
