Avant d'aller plus loin, il faut définir ce que nous entendons par dipôle électrique.
Nous avons introduit dans les chapitres précédents les densités volumiques de charges et de courants dans un milieu en moyennant les charges microscopiques sur un volume petit macroscopiquement mais grand microscopiquement.
De la même façon, il est possible de quantifier pour un petit volume le déséquilibre et la répartition des charges positives et charges négatives.
Si nous prenons une origine
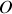et un ensemble de
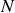charges positives
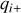présentes aux points
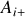et
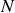charges négatives
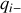présentes aux points
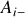le moment dipolaire
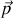de cette distribution de charges est défini par
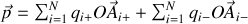
soit comme barycentre des lieux des charges pondérés par les valeurs algébriques de celles-ci. Il est alors facile de généraliser pour une distribution continue de charges en remplaçant les sommes discrètes par des intégrales, comme nous l'avons fait pour les densités de charges et de courants.
Cas de deux charges égales et opposées
Par ailleurs, dans le cas simple de deux points
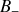et
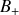portant des charges égales et opposées
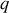, définissant un dipôle électrique, il vient
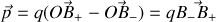
Dans ce dernier cas particulier, calculons le potentiel électrique
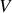régnant en un point
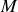
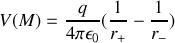
avec
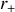la distance du point
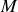au point
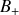, et
la distance du point
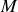au point
.
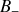Si nous introduisons le point
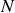comme point milieu de
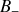et
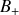on a
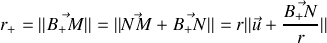
et
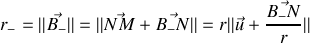
en notant
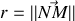et
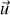vecteur unitaire dans la direction
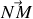. Par conséquent
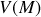se réexprime sous la forme
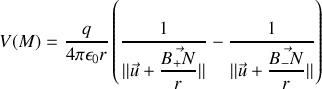
Or
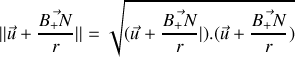
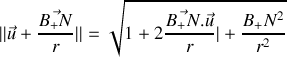
et de même pour la charge négative.
Remarque :
Si nous considérons désormais que la distance
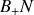est petite par rapport à
, il est possible de négliger au premier ordre le terme quadratique et de faire un développement limité au premier ordre de l'inverse de la racine carrée.
Avec le même raisonnement pour la charge négative, en tenant compte du signe, il vient
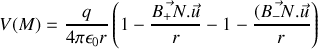
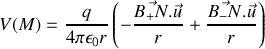
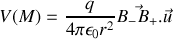
et finalement
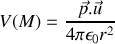
formule élégante justifiant l'introduction du moment dipolaire.
Rappel :
Cette formule n'est valable que si
est grand devant la distance des deux charges.
En nous plaçant en coordonnées polaires appropriées d'origine
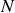, avec
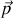suivant l'axe
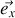et
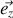orthogonal au plan
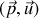il vient
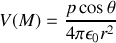
et si nous calculons le champ électrique au point
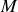
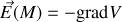en coordonnées polaires il apparaît
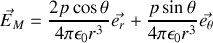
soit encore de façon intrinsèque en se débarrassant des vecteurs unitaires
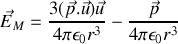
Cas du dipôle rigide
Il est alors facile d'établir l'énergie potentielle
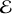d'un dipôle rigide en interaction avec un champ
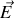dérivant d'un potentiel
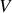
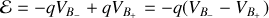
or
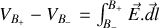
encore une fois si les deux charges sont proches on peut faire l'approximation
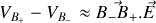
ainsi il vient
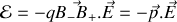
De la même façon on peut établir que le dipôle subit un moment résultant des forces électriques sur chacune des charges
