Nous avons vu que l'apparition de charges de polarisation dans un matériau diélectrique est causée par l'application d'un champ électrique extérieur
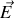. Comme usuellement en physique, nous allons dans un premier temps proposer de relier cause et conséquence par une relation linéaire. Ainsi, si nous pouvons écrire (ce qui n'est pas vrai dans l'absolu)
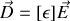
avec
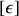une matrice
, le matériau sera dit linéaire diélectriquement. La matrice
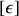sera dite opérateur pemittivité diélectrique.
Remarque :
Si cette matrice est proportionnelle à la matrice unité, on dira que le milieu est isotrope (dans ce cas le vecteur excitation électrique est parallèle au champ électrique), et si la constante de proportionnalité ne varie pas avec la position, on dira que le milieu est homogène.
En résumé pour un milieu linéaire, homogène et isotrope (DLHI)
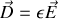
avec
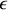une constante.
Dans ce cas puisque
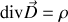
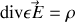
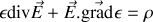
et si
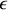est constant (milieu homogène spatialement) le second terme est nul et il reste
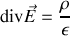
Équation très proche de l'équation de Maxwell-Gauss. Tout ce que nous avons démontré dans le vide reste donc vrai à condition de remplacer
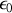par
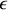qui s'exprime d'ailleurs dans la même unité.
On définit ainsi la permittivité relative
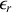du milieu, sans dimension, telle que
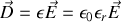
La conséquence en est pour la densité de polarisation que
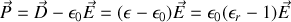
En posant
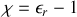on obtient de nouveau une relation linéaire entre cause et conséquences
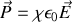
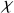sera appelée susceptibilité diélectrique.
Remarque :
Si désormais nous reprenons le calcul de la capacité
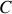d'un condensateur plan formé de deux électrodes de surface
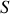éloignées d'une distance
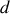et séparées par un milieu de permittivité relative
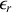nous trouvons bien
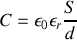
avec un raisonnement similaire à celui employé dans le vide.
Complément :
On voit que la capacité augmente en présence d'un diélectrique d'où l'intérêt de développer des matériaux à permittivité très élevée et champ de claquage important, pour aider au stockage de l'énergie dans des véhicules hybrides par exemple.
