Notation complexe
Supposons, pour simplifier, que nous nous trouvons désormais en régime sinusoïdal forcé, comme par exemple nous pouvons souvent nous ramener en utilisant l'analyse de Fourier.
Ainsi si le champ électrique local vaut
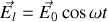
en régime forcé le dipôle électrique local suivra avec un certain déphasage
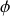
Ainsi
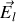et
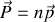seront colinéaires mais déphasés.
Par conséquent comme
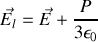
et
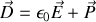
de même
,
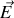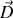et
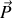seront colinéaires et déphasés.
Si l'on pose
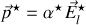
pour le choix de la représentation complexe
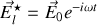
avec
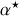polarisabilité électronique complexe, il vient naturellement que les coefficients sont les mêmes qu'en régime statique. L'existence éventuelle de parties imaginaires dans les coefficients traduit le déphasage entre les champs.
Par convention on prendra positives les parties imaginaires des différents coefficients et
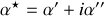
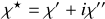
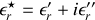
Remarquons que dans le cas du choix inverse
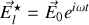
alors on aurait
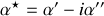
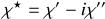
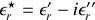
Polarisation par déformation en régime variable
Théorie de l'électron élastiquement lié
Reprenons l'équation de Newton pour un électron supposé élastiquement lié, de masse
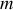soumis à une force de rappel
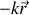et une force de freinage
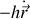
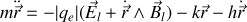
en incluant désormais la contribution magnétique à la force de Lorentz.
Remarque :
Pour une onde électromagnétique plane le champ magnétique est
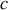fois plus petit que le champ électrique dans le vide et donc souvent négligeable.
La force de freinage est issue d'une part des chocs entre particules, et donc négligeable si le milieu est peu dense, et d'autre part du rayonnement de freinage émis par toute particule accélérée (voir les exercices et le cours correspondants). Ce terme est à prendre en compte aux fortes accélérations, typiquement pour une fréquence comprise entre
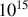et
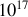Hz, donc dans le domaine des rayonnements allant de l'ultraviolet aux rayons X. Au delà il faudrait introduire la relativité dans les équations car les vitesses s'approcheraient de celle de la lumière.
Il existe un effet similaire pour les ions d'un cristal ionique, pour des fréquences divisées par le rapport de la masse de l'ion sur celle de l'électron, donc typiquement entre
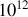et
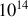Hz donc dans l'infrarouge proche.
Pour l'atome d'hydrogène, à un électron, en posant derechef
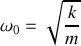
on obtient donc
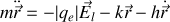
en régime forcé par
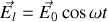
en posant
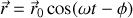
il vient
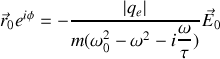
en posant
.
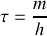Le vecteur dipôle électrique, en négligeant le mouvement des noyaux, vaut
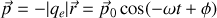
comme en notation complexe
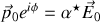
il vient
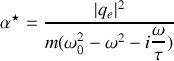
Milieu peu dense
Dans le cas d'un milieu dilué où l'amortissement est faible, on peut négliger le terme imaginaire au dénominateur. Dans ce cas
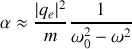
L'électron se comporte alors comme un oscillateur faiblement amorti, et l'on est dans une région de transparence. De plus on retrouve la polarisabilité statique si
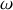est faible face à
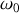. Au contraire au voisinage de
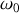on a une résonance et l'électron effectue des oscillations de forte amplitude ; les accélérations sont fortes et le rayonnement de freinage n'est plus négligeable. On dit que l'on est dans une région d'absorption et la polarisabilité devient complexe.
Région d'absorption
Cette polarisabilité avait été définie comme
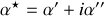
par conséquent
comme
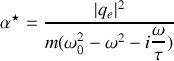
on obtient
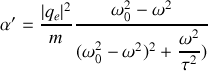
et
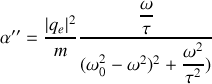
on peut facilement montrer que
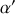est extrémal pour
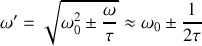
et qu'aux extréma on atteint les valeurs
.
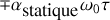alors que
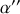est extrémal pour
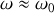au premier ordre en
.
On a donc une région d'absorption importante autour de
.
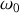Influence de la densité
Nous avions montré plus haut que
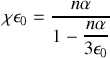
Au premier ordre pour les faibles densités, en étendant aux complexes on a donc
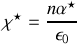
ce qui donnera une susceptibilité ou une permittivité imaginaire non nulle dans la zone d'absorption.
Si par contre on tient compte de la densité au dénominateur, on voit qu'on aura un décalage de la zone d'absorption à mesure que la densité augmente.
Atome à plusieurs électrons
Si nous considérons désormais que l'atome ou la molécule étudiée possèdent plusieurs électrons, en première approximation on peut sommer sur les niveaux électroniques
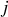de population
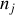possédant chacun une fréquence de résonance
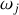pour obtenir
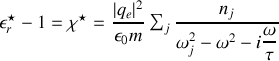
Dans le cas d'un cristal ionique dont chaque atome a une masse
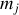et présente une charge
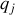et un temps caractéristique
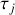on obtient de même
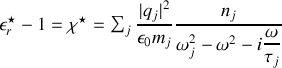
On peut inclure les électrons comme l'une des charges
de ce dernier système ce qui simplifiera les équations.
Application à l'optique
Indice complexe
Considérons un système formé de vide pour
et d'un milieu infiniment long pour
.
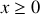Supposons qu'une onde électromagnétique plane polarisée rectilignement suivant
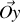frappe l'interface.
Dans le vide le champ électrique vaut donc
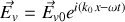
avec un vecteur d'onde
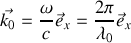
et dans le milieu
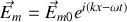
avec un vecteur d'onde
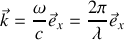
Par convention l'indice optique
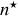est égal au rapport de la célérité de la lumière dans le vide par rapport à celle dans le milieu. Comme par continuité temporelle du champ électrique à l'interface les pulsations sont les mêmes dans le vide et dans le milieu on a
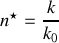
La résolution des équations de Maxwell dans le vide et dans le milieu donne facilement
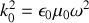
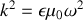
or
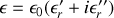
donc
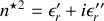
si l'on décompose
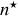en parties réelles et imaginaires selon
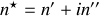
on obtient
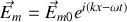
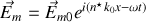
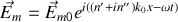
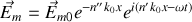
on a donc atténuation de l'onde dans le milieu, avec perte d'énergie par rayonnement des électrons des atomes par exemple.
La solution physique de
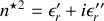correspond donc à
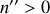sinon on aurait amplification de l'onde dans le milieu.
Le plus facile pour calculer
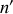et
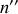est de passer en notation trigonométrique selon
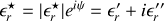
Rappel :
Nous avions choisi
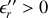donc
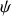est compris entre
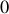et
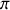. Par conséquent
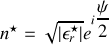
et on a bien
.
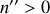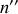est appelé indice d'extinction et
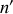l'indice de réfraction ou l'indice de propagation de phase.
Rappel :
On peut avoir plusieurs bandes d'absorption optique centrées autour des fréquences de résonance ioniques ou électroniques.
Régions de transparence : relation de Sellmeier
Rappelons que nous avions trouvé
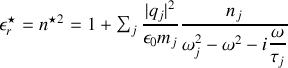
Dans les régions de transparence, loin des pulsations de résonance, on aura donc
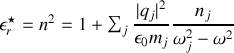
Si on exprime ce résultat en fonction des longueurs d'onde
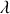et
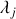telles que
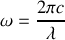
et
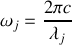
on obtient
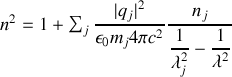
soit en introduisant des coefficients
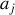pour simplifier l'expression
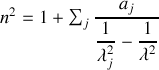
avec un peu d'algèbre
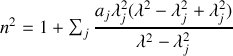
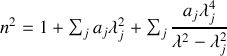
formule que l'on peut résumer sous la forme de la relation de Sellmeier
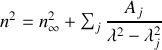
formule qui donne la variation de l'indice d'un milieu transparent en fonction de la longueur d'onde, et donc la relation de dispersion dans le milieu permettant d'expliquer des phénomènes tels que la décomposition de la lumière par un prisme par exemple.
Formule de Cauchy
Dans le domaine de la lumière visible, la fréquence du rayonnement est bien inférieure à la fréquence de résonance des électrons, et donc si le milieu est transparent on a
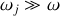
donc
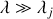
et on peut simplifier la relation de Sellmeier en
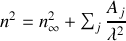
et si l'on ne conserve que la résonance électronique en négligeant les résonances ioniques
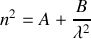
ce qui constitue la formule de Cauchy, souvent suffisante en pratique pour modéliser la variation de l'indice d'un verre optique en fonction de la longueur d'onde de la lumière.
