Dans les paragraphes précédents, nous avons modélisé les milieux diélectriques par un effet moyen des molécules. On peut aller cependant un peu plus loin en séparant les contributions moyennes des molécules constituant le milieu de leurs contributions locales.
Méthode de Lorentz
Ainsi, si nous considérons un milieu diélectrique où règnent un champ électrique
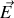et un vecteur excitation électrique
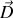homogènes (comme au sein d'un grand condensateur par exemple) nous pouvons autour d'un point
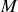donné définir une sphère d'un rayon
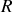petit mais décelable à l'échelle microscopique ; l'étude des molécules à l'extérieur de cette sphère pourra donc se faire d'un point de vue macroscopique comme dans les paragraphes précédents.
Par contre l'étude des molécules situées à l'intérieur de la sphère relève d'une étude microscopique.
Le champ
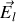régnant au centre de la sphère est donc en vertu du principe de superposition somme du champ
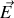créé par les charges libres (sur les armatures du condensateur par exemple), du champ
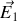créé par les charges liées au diélectrique à l'extérieur de la sphère, et du champ
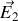créé par les molécules présentes dans la sphère.
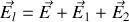
Or si nous supposons par exemple que la polarisation d'ensemble
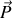de la sphère microscopique est dirigée suivant la direction
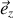des coordonnées polaires, alors le champ
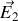créé par les charges liées au diélectrique à l'intérieur de la sphère est somme des contributions des charges surfaciques
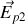telles que nous les avons vues au paragraphe précédent, et des contributions des charges volumiques.
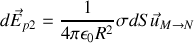
or
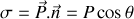
Et par symétrie les contributions à
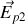de part et d'autre de l'axe
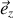s'additionnent pour donner une résultante double suivant ce même axe pondérée par un
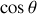en projection.
En sommant sur la moitié de la sphère située par exemple pour les
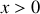il vient
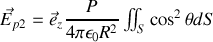
or sur la demi-sphère
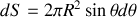
et finalement
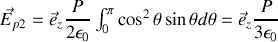
en faisant le changement de variable trivial
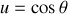
Ainsi le champ total régnant dans la sphère au point
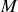vaut
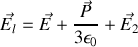
Remarque :
Dans un milieu gazeux, liquide ou solide totalement amorphe assimilable à une distribution de dipôles totalement irrégulière le champ
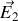est nul comme nous l'avons expliqué dans les paragraphes précédents, de même que pour un réseau régulier cubique dont
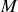serait un noeud.
Polarisabilité d'un diélectrique
Rappel :
Nous avons défini la polarisabilité
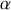d'un dipôle de moment
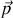soumis à un champ électrique local
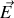par
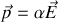
Si
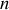dénote le nombre de dipôles par unité de volume alors
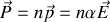
Polarisabilité électronique
Rappel :
Le moment dipolaire d'un nuage de charges
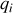situées aux positions
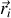vaut
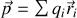
Pour un noyau d'hydrogène par exemple
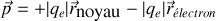
L'électron étant environ 1836 fois plus léger que le noyau, l'amplitude de son mouvement est bien plus importante, et on peut donc négliger en première approximation le mouvement du noyau sous l'effet d'un champ extérieur (c'est une des versions de l'approximation de Born-Oppenheimer)
Ainsi en simplifiant les notations
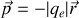
Dans la théorie simplifiée classique de l'électron élastiquement lié nous pouvons écrire l'équation de Newton pour l'électron de masse
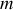soumis à une force de rappel
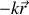et une force de freinage
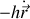
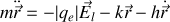
La solution stationnaire pour
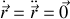vaut
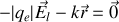
donc
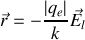
et
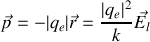
Si nous introduisons la pulsation
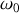de l'oscillateur harmonique correspondant à la force de rappel élastique
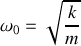
donc
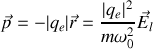
donc la polarisabilité électronique statique vaut
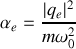
Pour aller plus loin et préciser la valeur de la pulsation à partir de premiers principes, un traitement quantique de l'électron est nécessaire.
Polarisabilité ionique
Dans le cas d'un cristal ionique on obtient un résultat tout à fait similaire en sommant sur les contributions des ions.
Polarisabilité d'orientation pour des molécules polaires
Nous avons vu que dans un milieu désordonné constitué de molécules polaires, la polarisation moyenne est nulle par suite du désordre, en champ nul. Par contre si le champ local
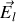est non nul, on va observer une tendance à l'orientation de
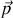dans le sens de
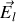afin de minimiser l'énergie potentielle d'interaction
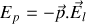entre les dipôles et le champ. Cet effet est cependant contrarié par l'agitation thermique.
Quantitativement, supposons qu'il y a
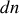dipôles par unité de volume, contenus dans l'angle solide
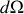défini autour de la direction
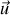. La densité de dipôles vaut
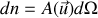
Il se trouve que l'on peut en théorie cinétique classique (voir l'introduction du cours de thermodynamique correspondant) exprimer la probabilité
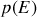de trouver un système dans l'état d'énergie
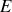(l'état d'énergie la plus basse possible étant pris à
)
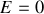par
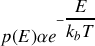
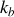étant la constante de Boltzmann et
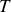la température absolue du thermostat entourant le système.
Les probabilités étant normalisées à
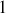on obtient ainsi la constante de proportionnalité.
Ici nous aurons
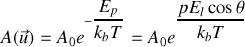
si
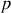dénote la norme de
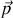et
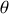l'angle entre
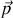et
.
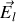Alors
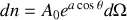
avec
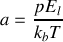
Par symétrie le vecteur polarisation résultant
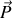de norme
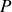est colinéaire à
.
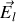Par conséquent
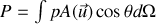
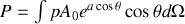
or l'élément d'angle solide vaut en intégrant sur l'angle polaire
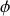
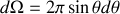
soit
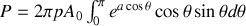
or
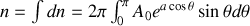
de cette dernière équation nous tirons
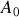et finalement
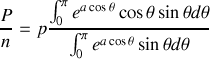
ou
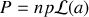
avec
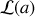qui sera appelée fonction de Langevin.
Ainsi la polarisation moyenne est égale au produit de la densité de dipôles par unité de volume, de la valeur absolue d'un dipôle, et de cette fonction de Langevin dont nous pouvons remarquer qu'elle est égale au quotient de la dérivée d'une fonction
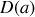par cette même fonction
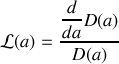
Nous reconnaissons une dérivée logarithmique
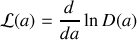
avec
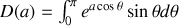
En effectuant le changement de variable trivial
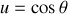, comme
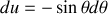
il vient
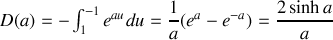
et
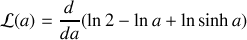
soit
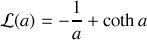
Attention :
La fonction de Langevin tend vers
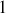quand
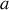tend vers l'infini (basses températures par exemple), et vers
quand
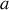tend vers
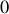(hautes températures, revoir la définition de
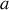plus haut) comme le montre un développement limité que nous laisserons faire au lecteur.
Ainsi comme nous l'avions discuté qualitativement pour les hautes températures l'agitation thermique rend la moyenne de la polarisation d'orientation nulle. Par contre par exemple pour la température ambiante (
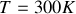), même pour un champ
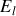intense de l'ordre de
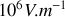
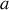est très petit et on peut assimiler
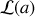à sa limite.
Il vient donc dans ce cas des basses températures
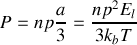
avec une polarisation colinéaire au champ local.
La polarisabilité d'orientation vaut donc
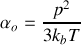
Rappelons qu'elle se superpose aux polarisabilités ioniques et électroniques.
Relation entre susceptibilité et polarisabilité
La polarisation totale
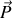s'exprime soit en fonction du champ total
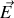soit en fonction du champ local
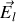. Nous avons par ailleurs montré que
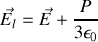
Comme cette polarisation s'exprime soit en fonction de la susceptibilité
soit en fonction de la polarisabilité
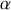
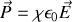
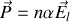
en comparant ces deux formules et l'expression du champ local on obtient avec un peu d'algèbre
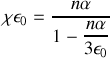
Pour un milieu peu dense on peut négliger le terme correctif au dénominateur et on obtient
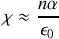
et on retrouve bien que le champ local est proche du champ total.
Formule de Clausius-Mossoti
Nous pouvons a contrario reprendre la formule précédente entre susceptibilité et polarisation pour trouver
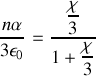
Rappel :
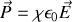
et que le vecteur déplacement électrique
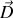vaut
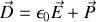
donc
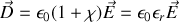
et
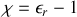
ainsi
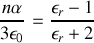
ce qui constitue la formule de Clausius-Mossoti.
Remarque :
La polarisabilité
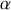dépend de la température et que la densité
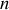dépend de la pression et de la température. Par conséquent la permittivité relative
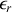dépend elle aussi de ces mêmes paramètres.
On peut également exprimer la densité moléculaire
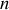en fonction de la densité
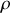, du nombre d'Avogadro
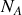et de la masse molaire
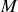
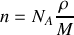
alors
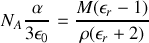
Si nous supposons que polarisabilités électroniques et ioniques sont constantes, en reprenant la formule pour la polarisabilité totale incluant la dépendance de la polarisabilité d'orientation en fonction de la température
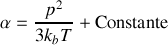
on trouve donc une dépendance linéaire pour
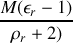
en fonction de cette même température, plus ou moins importante en fonction du carré de la valeur du moment dipolaire
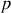. Pour une molécule non polaire comme le méthane par exemple on peut prédire que
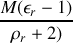est à peu près indépendant de la température.
